Phương trình 2^23x^2 .2^x -1024^x^2 +23x^3=10x^2-x có tổng các nghiệm gần nhất

Câu hỏi:

Phương trình $2^{23 x^{3}} . 2^{x} - 1024^{x^{2}} + 23 x^{3} = 10 x^{2} - x$ có tổng các nghiệm gần nhất với số nào dưới đây

A. 0,50

B. 0,35

C. 0,40

D. 0,45

Trả lời:

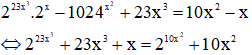
Xét hàm số:

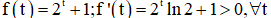
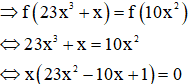
Theo vi-et cho phương trình bậc ba ta có:

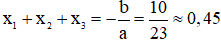
Đáp án cần chọn là: D.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tìm giá trị của a để phương trình ${(2 + \sqrt{3})}^{x} + (1 - a) {(2 - \sqrt{3})}^{x}$ $- 4 = 0$ có 2 nghiệm phân biệt thỏa mãn: $x_{1} - x_{2} = \log_{2 + \sqrt{3}} 3$ , ta có a thuộc khoảng:

Xem lời giải »

Câu 2:

Tìm tập hợp tất cả các tham số m sao cho phương trình $4^{x^{2} - 2 x + 1} - m . 2^{x^{2} - 2 x + 1} + 3 m - 2 = 0$ có 4 nghiệm phân biệt.

Xem lời giải »

Câu 3:

Có bao nhiêu số nguyên m thuộc $[- 2020; 2020]$ sao cho phương trình $4^{{(x - 1)}^{2}} - 4 m . 2^{x^{2} - 2 x} + 3 m - 2 = 0$ có bốn nghiệm phân biệt?