Phương trình 2^log 5 (x+3)=x có tất cả bao nhiêu nghiệm
Câu hỏi:
Phương trình có tất cả bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 0
Trả lời:
Điều kiện: x > - 3
Do 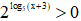 nên để phương trình có nghiệm thì x > 0
nên để phương trình có nghiệm thì x > 0
Lấy logarit cơ số 2 của hai vế phương trình, ta được 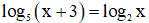
Đặt
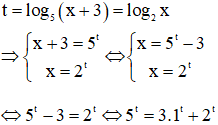
Chia hai vế phương trình cho , ta được 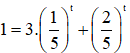
Đây là phương trình hoành độ giao điểm của đường thẳng y = 1 (hàm hằng) và đồ thị hàm số 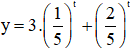 (hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến)
(hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến)
Do đó phương trình có nghiệm duy nhất. Nhận thấy t = 1 thỏa mãn phương trình
Với 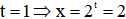 (tm)
(tm)
Vậy phương trình có nghiệm duy nhất
Đáp án cần chọn là: A.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm giá trị của a để phương trình có 2 nghiệm phân biệt thỏa mãn: , ta có a thuộc khoảng:
Xem lời giải »
Câu 2:
Tìm tập hợp tất cả các tham số m sao cho phương trình có 4 nghiệm phân biệt.
Xem lời giải »
Câu 3:
Có bao nhiêu số nguyên m thuộc sao cho phương trình có bốn nghiệm phân biệt?
Xem lời giải »
Câu 4:
Các giá trị thực của tham số m để phương trình: có nghiệm thuộc khoảng (-1; 0) là
Xem lời giải »
Câu 5:
Tìm m để phương trình có nghiệm
Xem lời giải »
Câu 6:
Tính S là tổng tất cả các nghiệm của phương trình
Xem lời giải »
Câu 7:
Phương trình có tổng các nghiệm bằng:
Xem lời giải »
Câu 8:
Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất
Xem lời giải »
nên để phương trình có nghiệm thì x > 0
(hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến)
(tm)

