Phương trình 3.25^x-2 + (3x - 10) .5^x-2 + 3 – x = 0 có tất cả bao nhiêu nghiệm

❮ Bài trước Bài sau ❯

Câu hỏi:

Phương trình 3.25^x-2+ (3x - 10) .5^x-2+ 3 – x = 0 có tất cả bao nhiêu nghiệm?

A. 1

B. 2

C. 3

D. 4

Trả lời:

Chọn B.

Đặt t = 5^x-2 > 0, phương trình trở thành 3t²+ (3x - 10) t + 3 – x = 0 (*)

Ta coi đây là phương trình bậc hai ẩn t và có

∆ = (3x - 10) ² – 4.3( 3 - x) = (3x - 8)²

Suy ra phương trình(*) có hai nghiệm: t = 1/3 hoặc t = 3 - x.

Với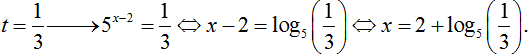

Với t = 3 - x thì 5^x-2= 3 - x. Dễ thấy x = 2 là nghiệm duy nhất (Vế trái là hàm đồng biến, vế phải là hàm nghịch biến).

Vậy phương trình đã cho có hai nghiệm.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Xét các số thực dương thỏa mãn $\log_{3} \frac{1 - x y}{x + 2 y} = 3 x y + x + 2 y - 4$ . Tìm giá trị nhỏ nhất S_min của S = x + y

Xem lời giải »

Câu 2:

Cho hai số thực dương a; b thỏa mãn log₂(a + 1) + log₂(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là

Xem lời giải »

Câu 3:

Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất P_min của biểu thức $P = \log_{\frac{a}{b}}^{2} (a^{2}) + 3 \log_{b} \frac{a}{b}$

Xem lời giải »

Câu 4:

Số nghiệm của phương trình: $9^{x + \log_{3} 2} - 2 = 3^{x + \log_{3} 2}$ là

Xem lời giải »

Câu 5:

Biết phương trình 2^x+1. 5^x= 15 có nghiệm duy nhất dạng alog5 + blog3 + clog2 với a; b; c nguyên . Tính S = a + 2b + 3c.

Xem lời giải »

Câu 6:

Phương trình $2^{x - 3} = 3^{x^{2} - 5 x + 6}$ có hai nghiệm $S = (- 1; \sqrt{5})$ trong đó x₁< x₂, hãy chọn phát biểu đúng

Xem lời giải »

Câu 7:

Biết rằng phương trình ${(2 + \sqrt{5})}^{x + 1} = 8 {(\sqrt{5} - 2)}^{2 x - 1}$ có nghiệm duy nhất dạng $\log_{2 + \sqrt{5}} a$ , với a là số thực dương. Mệnh đề nào dưới đây là đúng?

Xem lời giải »

Câu 8:

Giải phương trình $3 {(\sqrt{5} - 2)}^{x + 1} = {(9 + 4 \sqrt{5})}^{2 x}$

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Phương trình 3.25^x-2 + (3x - 10) .5^x-2 + 3 – x = 0 có tất cả bao nhiêu nghiệm

Xem thêm bài tập Toán có lời giải hay khác: