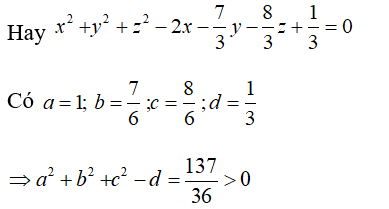Phương trình nào dưới đây là phương trình của một mặt cầu? x^2 + y^2 + z^2
Câu hỏi:
Phương trình nào dưới đây là phương trình của một mặt cầu?
A. - 2x + 4y - 8z + 25 = 0
B. - 2x - 4y - 6z + 15 = 0
C. 3 - 6x - 7y - 8z + 1 = 0
D. + 10 = 0
Trả lời:
Đáp án C
Sử dụng phương trình - 2ax - 2by - 2cz + d = 0 là phương trình của một mặt cầu khi và chỉ khi - d > 0
+ Phương án A và B không thỏa mãn điều kiện - d > 0
+ Phương án C: 3 - 6x - 7y - 8z + 1 = 0
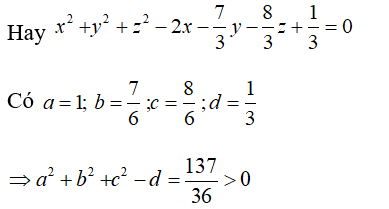
Nên đây có là phương trình mặt cầu.
+ Phương án D: + 10 = 0
⇔ = -10 nên không là phương trình mặt cầu.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho hai vectơ = (1; -2; 2), = (-2; m - 3; m). Với những giá trị nào của m thì hai vectơ và có độ dài bằng nhau?
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:
Xem lời giải »
Câu 3:
Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?
Xem lời giải »
Câu 4:
Cho hai vectơ thay đổi nhưng luôn thỏa mãn 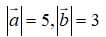
Giá trị lớn nhất của 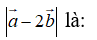
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
+ 6x - 8y + 15z - 3 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
Xem lời giải »
Câu 6:
Trong không gian Oxyz, cho mặt cầu (S) có đường kính AB với A(-2;-4;3), B(4;2;0). Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
Xem lời giải »
Câu 7:
Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:
Xem lời giải »
Câu 8:
Cho (S) là mặt cầu có tâm I(1;2;4) và đi qua điểm M(-1;4;3). Khẳng định nào dưới đây sai?
Xem lời giải »