Rút gọn biểu thức A= log 3 x.log 2 3+log 5 x.log 4 5( x> 0) ta được

Câu hỏi:

Rút gọn biểu thức A= log₃x.log₂3+ log₅x.log₄5 ( x> 0) ta được:

C.A= 2log₂x

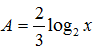
Trả lời:

Áp dụng công thức : log_ab. log_bc= log_ac, ta có:

A= log₃x.log₂3+ log₅x.log₄5= log₂x+ log₄x

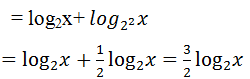
Chọn A.

Câu 1:

Với giá trị nào của x thì biểu thức $A = \log_{\frac{1}{2}} \frac{x - 1}{3 + x}$ xác định?

Câu 2:

Với giá trị nào của x thì biểu thức: f( x) = log₆( 2x- x²) xác định?

Câu 3:

Với giá trị nào của x thì biểu thức: f(x) = log₅( x³-x²-2x) xác định?

Câu 4:

Điều kiện xác định của biểu thức $T = l o g \sqrt{(x^{2} - 4) (x^{2} - 6 x + 9)}$ là

Câu 5:

Cho $\log_{3} x = 1 + \sqrt{2}$ . Tính giá trị biểu thức: $A = \log_{3} x^{3} + \log_{\frac{1}{3}} x + \log_{9} x^{2}$

Câu 6:

Tính giá trị của biểu thức $P = \log_{a} \frac{1}{b^{3}} \log_{\sqrt{b}} a^{3} (1 ≢ a; b > 0)$

Câu 7:

Tình giá trị của biểu thức $P = \log_{a} \frac{1}{b^{3}} \log_{\sqrt{b}} a^{3} (1 \neq a; b > 0)$

Câu 8:

Tính giá trị của biểu thức $P = \log_{\sqrt{a}} b^{3} . \log_{\sqrt{b}} a (1 \neq a, b > 0)$

Các dạng bài tập Toán lớp 12