Số nghiệm thực của phương trình 2f (x^2 - 1) - 5 = 0. A. 1 B. 3 C. 4 D. 2
Câu hỏi:
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên:
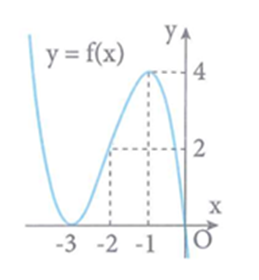
Số nghiệm thực của phương trình 2f (x2 – 1) – 5 = 0.
A. 1
B. 3
C. 4
D. 2.
Trả lời:
Đáp án đúng là: D
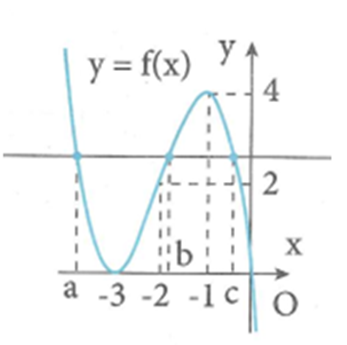
Ta có: 2f (x2 – 1) – 5 = 0
\( \Leftrightarrow f\left( {{x^2} - 1} \right) = \frac{5}{2}\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} - 1 = a < - 3\\{x^2} - 1 = b \in \left( { - 2; - 1} \right)\\{x^2} - 1 = c \in \left( { - 1;0} \right)\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} = a + 1 < - 2 < 0\\{x^2} = b + 1 < 0\\{x^2} = c + 1 > 0\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow {x^2} = c + 1 > 0\\ \Leftrightarrow x = \pm \sqrt {c + 1} \end{array}\)
Có 2 nghiệm thực
Vậy ta chọn đáp án D.

