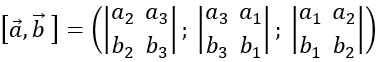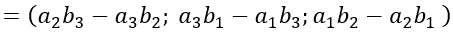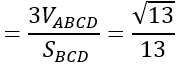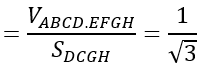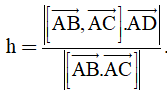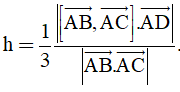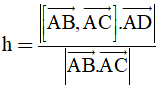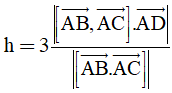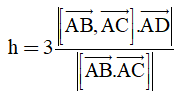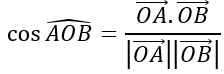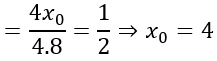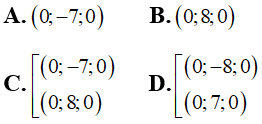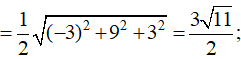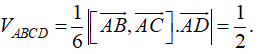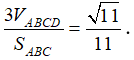Công thức tính Tích có hướng của hai vecto trong không gian cực hay - Toán lớp 12

---

Công thức tính Tích có hướng của hai vecto trong không gian cực hay

Với Công thức tính Tích có hướng của hai vecto trong không gian cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính Tích có hướng của hai vecto trong không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

1. Định nghĩa:

Trong không gian Oxyz cho hai vecto a→=(a₁;a₂;a₃ ) và b→=(b₁;b₂;b₃ ). Tích có hướng của hai vecto a→ và b→ , kí hiệu là [a→ , b→ ], được xác định bởi

Chú ý: Tích có hướng của hai vecto là một vecto, tích vô hướng của hai vecto là một số.

2. Tính chất

+ [a→, b→ ]⊥ a→ ; [a→ , b→ ]⊥ b→

+ [a→ , b→ ]=-[b→, a→ ]

+ [i→, j→ ]=k→ ; [ j→ , k→ ]= i→ ; [k→ , i→ ]= j→

+ |[ a→ , b→ ]|=| a→ |.| b→ |.sin⁡( a→ , b→ )

+ a→ , b→ cùng phương ⇔ [a→ , b→ ]= 0→ (chứng minh 3 điểm thẳng hàng)

3. Ứng dụng của tích có hướng (chương trình nâng cao)

+ Điều kiện đồng phẳng của ba vecto:

    a→ , b→ và c→ đồng phẳng ⇔[ a→ , b→ ]. c→ =0

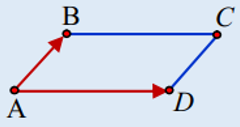
+ Diện tích hình bình hành ABCD:

    S_ABCD=|[AB→ ; AD→ ]|

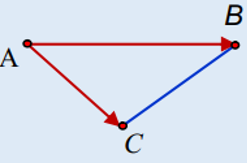
+ Diện tích tam giác ABC:

    S_ABC=1/2 |[AB→ ; AC→ ]|

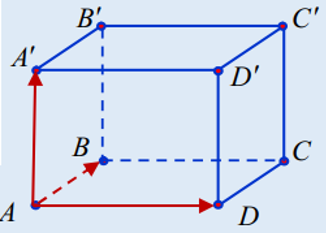
+ Thể tích khối hộp ABCD.A’B’C’D’:

    V_{ABCD.A'B'C'D'}=|[AB→; AD→ ]. AA'→ |

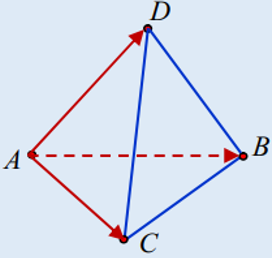
+ Thể tích tứ diện ABCD

    V_ABCD=1/3 |[AB→ ; AC→ ]. AD→ |

Ví dụ minh họa

Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(1; 0; 1), B(-1; 1; 2), C(-1; 1; 0), D(2; -1; -2).

a) Chứng minh rằng A, B, C, D là 4 đỉnh của một tứ diện.

b) Tính thể tích tứ diện ABCD. Suy ra độ dài đường cao của tứ diện qua đỉnh A

Hướng dẫn:

AB→ =(-2;1;1); AC→ =(-2;1; -1); AD→ =(1; -1; -3)

⇒[AB→ , AC→ ]=(-2;-4;0) ⇒[ AB→ , AC→ ]. AD→ =2≠0

⇒AB→ , AC→ , AD→ không đồng phẳng.

Vậy A, B, C, D là 4 đỉnh của một tứ diện.

b) V_ABCD=1/6 |[AB→ , AC→ ]. AD→ |=2/6=1/3

Ta có: BC→ =(0;0; -2), BD→ =(3; -2; -4)

⇒[ BC→ , BD→ ]=(-4; -6;0)⇒S_BCD=1/2 |[BC→ , BD→ ]|=√13

V_ABCD=1/3 d(A;(BCD)).S_BCD

⇒d(A;(BCD))

Bài 2: Trong không gian hệ trục tọa độ Oxyz, cho 4 điểm A(-3; 5; 15), B(0; 0; 7), C(2; -1; 4), D(4; -3; 0). Chứng minh AB và CD cắt nhau.

Hướng dẫn:

+ Ta có: AB→ =(3; -5; -8); AC→ =(5; -6; -11);

AD→ =(7; -8; -15), CD→ =(2; -2; -4)

⇒[ AB→ , AC→ ]=(7;-7;7) ⇒[ AB→ ,(AC) ⃗ ].(AD) ⃗=0

⇒ AB→ , AC→ , AD→ đồng phẳng.

⇒ A, B, C, D cùng thuộc một mặt phẳng (1)

+ [AB→ , CD→ ]=(4; -4;4) ≠0→ ⇔ AB→ , CD→ không cùng phương (2)

Từ (1) và (2) suy ra AB và CD cắt nhau.

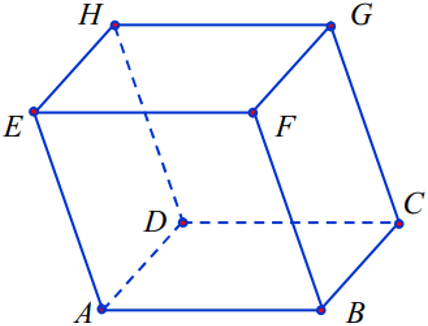
Bài 3: : Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.EFGH với A(1; 1; 1), B(2; 1; 2), E(-1; 2; -2), D(3; 1; 2). Tính khoảng cách từ A đến mặt phẳng (DCGH)

Hướng dẫn:

+ AB→=(1;0;1), AD→=(2;0;1), AE→=(-2;1; -3)

⇒[ AB→ , AD→ ]=(0;1;0)⇒[ AB→ , AD→ ]. AE→=1

⇒V_ABCD.EFGH=|[ AB→ , AD→ ]. AE→ |=1

+ S_AEFB=|[ AB→ , AE→ ]|=√3

⇒S_DCGH=S_AEFB=√3

V_ABCD.EFGH=d(A;(DCGH)).S_DCGH

⇒d(A;(DCGH))

B. Bài tập vận dụng

Bài 1: Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;2;1), B(1;0;2), C(-1;2;3). Diện tích tam giác ABC là:

   A. (3√5)/2   B. 3√5

   C. 4√5   D. 5/2

Lời giải:

Đáp án : B

Giải thích :

AB→ =(3; -2;1); AC→ =(1;0;2)⇒[AB→ , AC→ ]=(-4; -5;2)

S_ABC=1/2 |[AB→ , AC→ ]|=(3√5)/2

Bài 2: Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1). Thể tích của tứ diện ABCD là:

   A. 1   B. 2

   C. 1/3   D. 1/2

Lời giải:

Đáp án : D

Giải thích :

AB→ =(-1; 1;0); AC→=(-1;0;1); AD→=(-3;1; -1)

⇒[AB→ , AC→ ]=(1;1;1)⇒ AD→ . [AB→ , AC→ ]=-3

V_ABCD=1/6 |AD→ . [AB→ , AC→ ]|=1/2

Bài 3: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0). Bán kính đường tròn nội tiếp tam giác ABC là:

   A. √5   B. √3

   C. 4√2   D. 2√5

Lời giải:

Đáp án : A

Giải thích :

AB→=(-5; 0;-10); AC→=(3;0;-6); BC→=(8;0;4)

AB=5√5;AC=3√5;BC=4√5

S_ABC=1/2 |[ AB→ , AC→ ]|=30

Gọi r là bán kính đường tròn nội tiếp tam giác ABC, p là nửa chu vi tam giác

Ta có:

S=pr

⇒r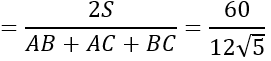=√5

Bài 4: Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD biết A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3). Thể tích tứ diện ABCD là:

   A. 3   B. 4

   C. 9   D. 6

Lời giải:

Đáp án : C

Giải thích :

AB→=(3; 6;3); AC→=(1;3;-2); AD→=(2;-2; 2)

⇒[ AB→ , AC→ ]=(-21;9;3)⇒ AD→ . [AB→ , AC→ ]=-54

V_ABCD=1/6 |AD→ . [AB→ , AC→ ]|=9

Bài 5: Trong không gian Oxyz cho tứ diện ABCD. Độ dài đường cao vẽ từ D của tứ diện ABCD cho bởi công thức nào sau đây:

   A.

   B.

   C.

   D.

Lời giải:

Đáp án : D

Bài 6: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC biết A(1;0;0), B(0;0;1), C(2;1;1). Độ dài đường cao của tam giác ABC kẻ từ A là:

   A. (2√30)/5   B. (√30)/5

   C. (√10)/5   D. (√6)/2

Lời giải:

Đáp án : B

Giải thích :

AB→=(-1; 0;1); AC→=(1;1;1)⇒[AB→ , AC→ ]=(-1;2;-1)

S_ABC=1/2 |[ AB→ , AC→ ]|=√6/2

BC=| BC→ |=√5

S_ABC=1/2 h.BC ⇒h=(2S)/BC=√(30)/5

Bài 7: Trong không gian với hệ toạ độ Oxyz, cho hình chóp S.OAMN với S(0;0;1), A(1;1;0), M(m;0;0), N(0;n;0). Trong đó m>0, n>0 và m+n=6. Thể tích hình chóp S.OAMN là:

   A. 1   B. 2

   C. 4   D. 6

Lời giải:

Đáp án : A

Giải thích :

OA→=(1;1;0), OM→=(m;0;0), ON→=(0;n;0), OS→=(0;0;1)

[ OA→ , OM→ ]=(0;0; -m)⇒ OS→ . [ OA→ , OM→ ]=(0;0; -m)

⇒V_S.OAM=1/6 |OS→ . [OA→ , OM→ ]|=m/6

[OA→ , ON→ ]=(0;0; m)⇒ OS→ . [OA→ , OM→ ]=(0;0; n)

⇒V_S.OAN=1/6 |OS→ . [OA→ , ON→ ]|=n/6

Ta có:

V_S.OAMN=m/6+n/6=(m+n)/6=1

Bài 8: Cho A(1;-2;0), B(3;3;2), C(-1;2;2), D(3;3;1). Thể tích của tứ diện ABCD bằng

   A. 3   B. 4

   C. 5   D. 6

Lời giải:

Đáp án : A

Giải thích :

AB→=(2;5-;2); AC→=(-2;4;2); AD→=(2;5;1)

⇒[AB→ , AC→ ]=(2; -8;18) ⇒ AD→ . [AB→ , AC→ ]=-18

V_ABCD=1/6 |AD→ . [AB→ , AC→ ]|=3

Bài 9: Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1). Độ dài đường cao AH của tứ diện ABCD là:

   A. 5   B. 6

   C. 7   D. 9

Lời giải:

Đáp án : D

Giải thích :

Áp dụng công thức:

tính được: h= 9

Bài 10: Trong không gian với hệ toạ độ Oxyz, cho A(1; 0; 0); B(0; 1; 0), C(0; 0; 1), D(1; 1; 1). Trong các mệnh đề sau, mệnh đề nào sai ?

   A. Bốn điểm A, B, C, D không đồng phẳng.

   B. Tam giác ABD là tam giác đều.

   C. AB⊥CD

   D. Tam giác BCD là tam giác vuông.

Lời giải:

Đáp án : D

Bài 11: Trong không gian với hệ toạ độ Oxyz, cho các điểm A(4;0;0), B(x₀;y₀;0) với x₀>0, y₀>0 sao cho OB=8 và góc AOBˆ=60⁰ . Gọi C(0;0;c) với c>0. Để thể tích tứ diện OABC bằng 16√3 thì giá trị thích hợp của c là:

   A. 6   B. 3

   C. √3   D. 6√3

Lời giải:

Đáp án : A

Giải thích :

OA→=(4;0;0), OB→=(x₀;y₀;0); OC→=(0;0;c)

OB=√(x₀²+y₀² )=8 ⇒y₀=4√3

OA→=(4;0;0); OB→=(4;4√3;0) ⇒[ OA→ , OB→ ]=(0;0;16√3)

⇒ OC→[ OA→ , OB→ ]=16c√3

V_ABCD=1/6 |OC→ [ OA→ , OB→]|=1/6.16c√3=16√3 ⇒c=6

Bài 12: Trong không gian với hệ toạ độ Oxyz, cho A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1). Thể tích của tứ diện ABCD bằng:

   A. 30   B. 40

   C. 50   D. 60

Lời giải:

Đáp án : A

Giải thích :

V_ABCD=1/6 |AD→ . [ AB→ , AC→ ]|=30

Bài 13: Trong không gian với hệ toạ độ Oxyz, cho A(2;1;-1), B(3;0;1), C(2;-1;3) điểm D thuộc Oy và thể tích tứ diện ABCD bằng 5. Tọa độ của D là:

Lời giải:

Đáp án : C

Giải thích :

D thuộc Oy ⇒ D(0;y;0)

AB→=(1;-1;2); AC→=(0;-2;4); AD→=(-2;y-1;1)

⇒ [AB→ , AC→ ]=(0; -4;-2) ⇒ AD→ . [AB→ , AC→ ]=2-4y

V_ABCD=1/6 |AD→ . [ AB→ , AC→ ]|=|2-4y|/6=5

⇒ |2-4y|=30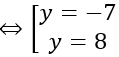

Bài 14: Trong không gian với hệ toạ độ Oxyz, cho A(0;0;2), B(3;0;5), C(1;1;0), D(4;1;2). Độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống (ABC) là:

   A. √(11)   B. √(11)/11

   C. 1   D. 11

Lời giải:

Đáp án : B

Giải thích :

Ta có AB→(3;0;3), AC→(1;1;-2), và AD→(4;1;0).

Dễ thấy [AB→, AC→]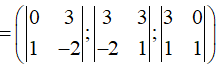=(-3;9;3),

nên S_ABC=1/2|[AB→, AC→]|

Vậy chiều cao hạ từ đỉnh D của tứ diện là

Bài 15: Trong không gian với hệ toạ độ Oxyz, cho A(0; 2; -2); B(-3; 1; -1);

C(4; 3; 0), D(1; 2; m). Tìm m để bốn điểm A, B, C, D đồng phẳng.

Một học sinh giải như sau:

   Bước 1: AB→=(-3;-1;1), AC→=(4;1;2), AD→= (1;0;m+2)

   Bước 2: [AB→, AC→]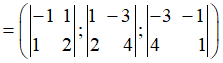=(-3;10;1)

    [AB→ , AC→ ]. AD→= 3+m+2 = m+5

   Bước 3: A, B, C, D đồng phẳng⇔[AB→, AC→]. AD→= 3+m+2 = m+5 = 0 ⇔ m= -5.

Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?

   A. Đúng.   B. Sai từ bước 1.

   C. Sai từ bước 2.   D. Sai từ bước 3.

Lời giải:

Đáp án : C

Giải thích :

Bước 2 sai. Phép tính đúng ở đây phải là [AB→, AC→] . AD→ = -3+m +2= m -1.

Bài 16: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có A(1;0;1), B(0;2;3), C(2;1;0). Độ dài đường cao của tam giác kẻ từ C là:

   A. √(26)   B. √(26)/2

   C. √(26)/3   D. 26

Lời giải:

Đáp án : C

Giải thích :

AB→(-1;2;2), AC→(1;1;-1). Độ dài đường cao kẻ từ C của tam giác ABC là:

d(C, AB)

Bài 17: Cho hình chóp S.ABCD biết A(-2;2;6), B(-3;1;8), C(-1;0;7), D(1;2;3). Gọi H là trung điểm của CD, SH⊥(ABCD). Để khối chóp S.ABCD có thể tích bằng 27/2(đvtt) thì có hai điểm S₁, S₂ thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm I của S₁S₂

   A. (0; 1; 5)    B. (1; 0; 5)

   C. (0; -1; -5)    D. (-1; 0; -5)

Lời giải:

Đáp án : A

Giải thích :

Ta có: AB→=(-1;-1;2); AC→=(1; -2;1) ⇒ [AB→; AC→ ]=(3;3;3)

⇒S_ABC=1/2 |[AB→ ; AC→ ]|=(3√3)/2

DC→=(-2; -2;4); AB→=(-1;-1;2) ⇒ DC→=2 AB→

⇒ ABCD là hình thang và S_ABCD=3S_ABC=(9√3)/2

V_ABCD=1/3 SH.S_ABCD=27/2 ⇒SH=3√3

Lại có H là trung điểm của CD ⇒H (0;1;5)

Gọi S (a; b; c) ⇒ SH→=(-a;1-b;5-c)

Do SH⊥(ABCD) nên SH→=k[ AB→ ; AC→]=(3k;3k;3k)

⇒3√3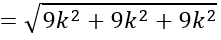⇒k=±1

Với k = 1 ⇒ SH→=(3;3;3)⇒S(-3; -2;2)

Với k = -1 ⇒ SH→=(-3;-3;-3)⇒S(3; 4;8)

⇒I(0;1;5)

Bài 18: Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Độ dài đường cao của tứ diện kẻ từ D là:

   A. 3   B. 1

   C. 2   D. 1/2

Lời giải:

Đáp án : A

Bài 19: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có A(1;0;1), B(0;2;3), C(2;1;0). Độ dài đường cao của tam giác kẻ từ C là:

   A. √(26)   B. √(26)/2

   C. √(26)/3   D. 26

Lời giải:

Đáp án : C

Bài 20: Trong không gian Oxyz, cho tứ diện ABCD có A(2;1;-1), B(3;0;1), C(2;-1;3) và D thuộc trục Oy. Biết V_ABCD=5 và có hai điểm D₁(0;y₁;0), D₂(0;y₂;0) thỏa mãn yêu cầu bài toán. Khi đó y₁+y₂ bằng

   A. 1   B. 0

   C. 2   D. 3

Lời giải:

Đáp án : A

Giải thích :

D thuộc trục Oy ⇒D(0;y;0)

AB→=(1; -1;2), AC→=(0; -2;4), AD→=(-2;y-1;1)

⇒[ AB→; AC→ ]=(0; -4; -2)⇒[AB→ ; AC→ ] . AD→=-4y+2

V_ABCD=1/6 |[ AB→ ; AC→ ] . AD→ |=1/6 |-4y+2|=5 ⇒y=-7;y=8

⇒D(0; -7;8) và D (0;8;0)

⇒ y₁+y₂= 1