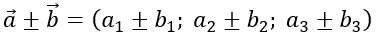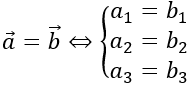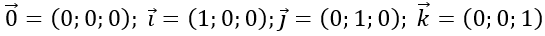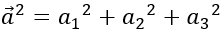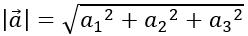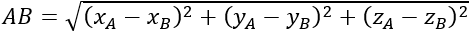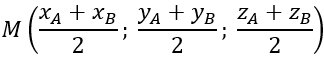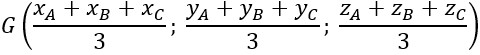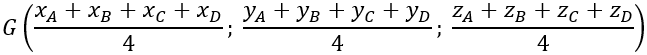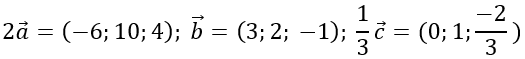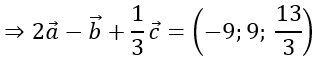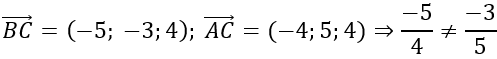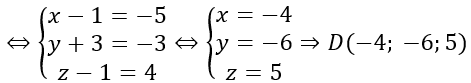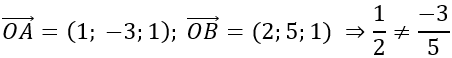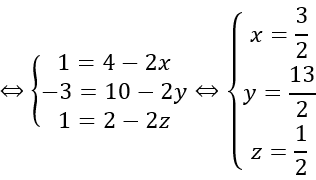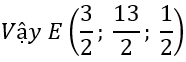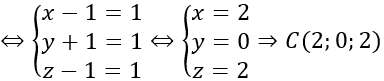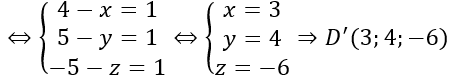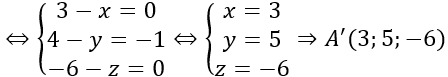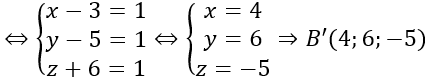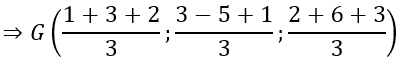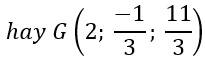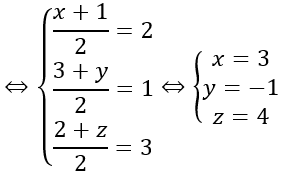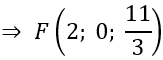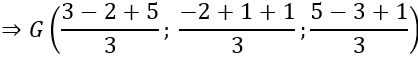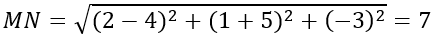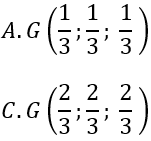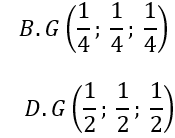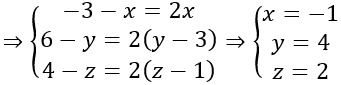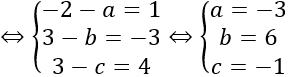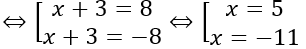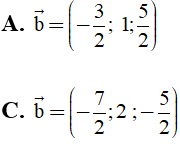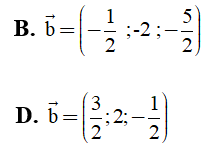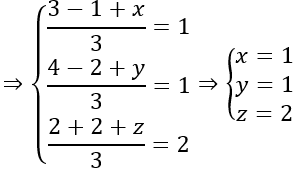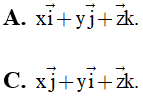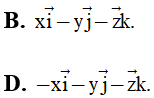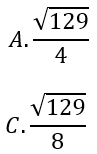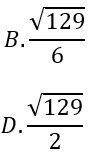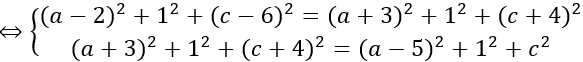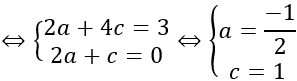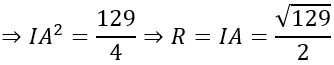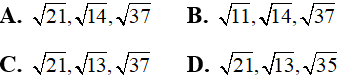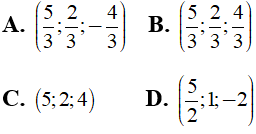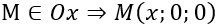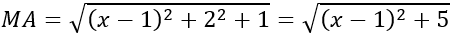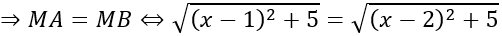Tìm tọa độ của vecto, của điểm cực hay - Toán lớp 12

---

Tìm tọa độ của vecto, của điểm cực hay

Với Tìm tọa độ của vecto, của điểm cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tọa độ của vecto, của điểm từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

1. Tọa độ của vecto

a) Định nghĩa

Ta gọi bộ ba số (x; y; z) là tọa độ của vecto u→ đối với hệ tọa độ Oxyz cho trước

     u→=(x;y;z)⇔u→=xi→+yj→+zk→

b) Tính chất

Trong không gian Oxyz, cho hai vecto a→ =(a₁;a₂;a₃ ) và b→ =(b₁;b₂;b₃ ); k∈R

+

+

+

+

+

+

2. Tọa độ của điểm

a) Định nghĩa

M(x;y;z)⇔OM→= xi→+yj→+zk→(x: hoành độ, y: tung độ, z: cao độ)

b) Tính chất

Cho A(x _A; y _A; z _A );B(x _B; y _B; z _B )

+ AB→ =(x_A-x_B;y_A-y_B;z_A-z_B )

+

+ Tọa độ trung điểm M của đoạn thẳng AB:

+

+ Tọa độ trọng tâm G của tam giác ABC:

+

+ Tọa độ trọng tâm G của tứ diện ABCD:

+

Ví dụ minh họa

Bài 1:Trong hệ trục tọa độ Oxyz, cho các vecto a→ =-3i→ +5j→ +2k→ ; b→ =(3;2; -1); c→ =3j→ -2k→ ; d→ =(5; -3;2)

a) Tìm tọa độ của các vecto a→ - 2b→ + c→ ; 3b→ -2c→ +d→

b) Tìm tọa độ của vecto 2a→ -b→ +1/3c→

c) Phân tích vecto d→ theo 3 vecto a→ ; b→ ; c→

Hướng dẫn:

a) a→ =(-3;5;2); 2b→ =(6;4; -2); c→ =(0;3; -2)

⇒ a→- 2 b→+ c→=(-9;4; 2)

3 b→=(9;6; -3); 2 c→=(0;6; -4); d→=(5; -3;2)

⇒3 b→-2 c→+ d→=(14; -3;7)

b)

c) giả sử d→=ma→+nb→+pc→

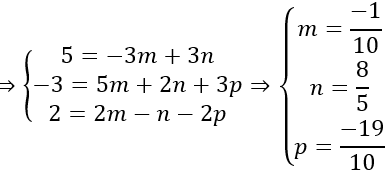
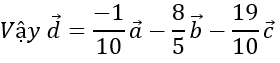
Bài 2:Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1; -3;1);B(2;5;1) và vecto OC→=-3 i→+2 j→+5 k→

a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

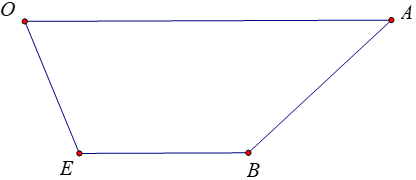
b) Tìm tọa độ điểm E sao cho tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.

c) Tìm tọa độ điểm M sao cho 3 AB→+2 AM→=3 CM→

Hướng dẫn:

a)

⇒BC→; AC→ không cùng phương hay A, B, C không thẳng hàng

Gọi D (x; y; z) ⇒AD→=(x-1;y+3;z-1)

ABCD là hình bình hành ⇔AD→=BC→

b)

Ta có:

⇒OA→; OB→ không cùng phương hay O, A, B không thẳng hàng.

Gọi E (x; y; z) ⇒EB→=(2-x;5-y;1-z)

Theo đề bài, tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.

⇒OA→=2EB→

c) Gọi M (x; y; z). Ta có:

AB→=(1;8;0)⇒3AB→=(3;24;0)

AM→=(x-1;y+3;z-1)⇒2AM→=(2x-2;2y+6;2z-2)

CM→=(x+3;y-2;z-5)⇒3CM→=(3x+9;3y-6;3z-15)

3AB→+2AM→=3CM→

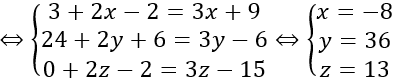
Vậy M(-8; 36; 13)

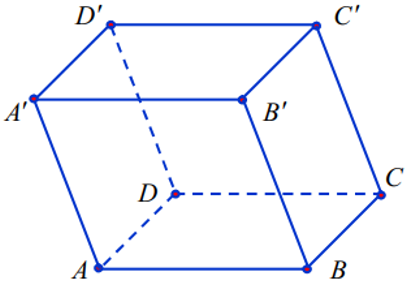
Bài 3:Trong không gian hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ biết A(1;0;1),B(2;1;2),D(1; -1;1);C^' (4;5; -5). Xác định tọa độ các đỉnh còn lại của hình hộp ABCD.A’B’C’D’.

Hướng dẫn:

+ Gọi C (x; y; z)

Ta có: AB→ =(1;1;1);DC→ =(x-1;y+1;z-1)

Tứ giác ABCD là hình bình hành ⇔AB→ =DC→

+ Gọi D’ (x; y; z)

Ta có: D^'C^'→ =(4-x;5-y; -5-z); DC→ =(1;1;1)

Tứ giác DCC’D’ là hình bình hành ⇔D^'C^'→=DC→

+ Gọi A’ (x; y; z)

Ta có: A^'D^'→=(3-x;4-y; -6-z); AD→=(0; -1;0)

Tứ giác ADD’A’ là hình bình hành ⇔A^'D^'→=AD→

+ Gọi B’ (x; y; z)

Ta có: D^'C^'→=(1;1;1);A^'B^'→=(x-3;y-5;z+6)

Tứ giác ABCD là hình bình hành ⇔A^'B^'→=D^'C^'→

Bài 4: Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có A(1; 3; 2), B(3; -5; 6), C (2; 1; 3).

a) Tìm tọa độ trung điểm M của cạnh AB

b) Tìm tọa độ trọng tâm G của tam giác ABC và hình chiếu của G lên Ox

c) Tìm tọa độ điểm N đối xứng với điểm A qua điểm C

d) Tìm tọa độ điểm F trên mặt phẳng Oxz sao cho |FA→+FB→+FC→ | nhỏ nhất

e) Tìm tọa độ điểm B’ đối xứng với điểm B qua trục tung.

Hướng dẫn:

a) M là trung điểm của cạnh AB

hay M(2; -1;4)

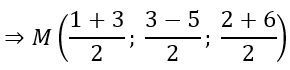
b) G là trọng tâm của tam giác ABC

Hình chiếu của G lên trục Ox là H (2; 0; 0)

c) Gọi N (x; y; z)

N đối xứng với A qua C ⇔ C là trung điểm của AN

⇒N(3; -1;4)

d) Ta có: |FA→ +FB→ +FC→ |=|3FG→ |=3FG

Do đó: |FA→ +FB→ +FC→ | nhỏ nhất ⇔ FG nhỏ nhất ⇔ F là hình chiếu của G lên mặt phẳng (Oxz)

e) Hình chiếu của B lên trục Oy là H (0; -5; 0)

B’ là điểm đối xứng với điểm B qua trục tung ⇔ H là trung điểm của đoạn BB’

⇒B'(-3; -5; -6)

B. Bài tập vận dụng

Bài tập Tìm tọa độ của vecto, của điểm (P1)

Bài 1: Trong không gian với hệ toạ độ Oxyz, cho ba vectơ: a→=(2; -5;3), b→=(0;2;-1),c→=(1;7;2). Tọa độ vectơ d→=a→-4b→-2c→ là:

   A. (0; - 27;3)    B. (1;2; - 7)

   C. (0;27;3)    D. (0;27; - 3)

Lời giải:

Đáp án : A

Giải thích :

a→=(2; -5;3), 4b→=(0;8; -4);2c→=(2;14;4)

d→=a→-4b→-2c→=(0; -27;3)

Bài 2:Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC với A(3;-2;5), B(-2;1;-3) và C(5;1;1). Trọng tâm G của tam giác ABC có tọa độ là:

   A. G(2;0;1)    B. G(2;1;-1)

   C. G(-2;0;1)    D. G(2;0;-1)

Lời giải:

Đáp án : A

Giải thích :

A (3; -2; 5), B(-2; 1; -3), C(5; 1; 1)

G là trọng tâm tam giác ABC

hay G(2;0;1)

Bài 3: Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(4;0;0), B(0;2;0), C(0;0;4) Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành:

   A. (4;-2;4)    B. (2;-2;4)

   C. (-4;2;4)    D. (4;2;2)

Lời giải:

Đáp án : C

Giải thích :

D (x; y; z) ⇒DC→=(-x; -y;4-z)

AB→=(-4;2;0)

ABCD là hình bình hành khi và chỉ khi AB→=DC→

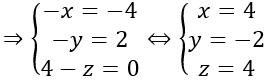
⇒D(4; -2;4)

Bài 4: Trong không gian với hệ tọa độ Oxyz. Tìm khoảng cách giữa hai điểm M(2;1;-3) và N(4;-5;0) ?

   A. 5    B. 6

   C. 7    D. 8

Lời giải:

Đáp án : C

Giải thích :

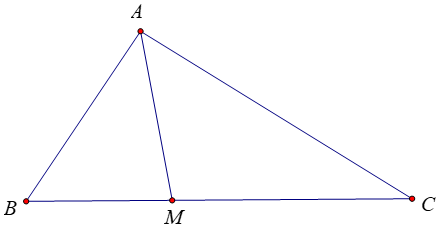
Bài 5: Trong không gian với hệ toạ độ Oxyz, gọi M, N lần lượt là trung điểm AB, CD với A(1;0;0), B(0;1;0), C(0;0;1), D(1;1;1). Khi đó trung điểm G của MN có tọa độ là:

Lời giải:

Đáp án : D

Giải thích :

A(1;0;0), B(0;1;0), C(0;0;1), D(1;1;1)

M là trung điểm của AB ⇒M(1/2;1/2;0 )

N là trung điểm của CD ⇒N(1/2;1/2;1)

G là trung điểm của MN ⇒ G(1/2; 1/2; 1/2)

Bài 6: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC A(2;0;0), B(0;3;1), C(-3;6;4). Gọi M là điểm trên cạnh BC sao cho MC=2MB. Độ dài đoạn AM bằng:

   A. 3√3    B. 2√7

   C. √29    D. √30

Lời giải:

Đáp án : C

Giải thích :

Gọi M(x; y; z)

CM→=(-3-x;6-y;4-z); MB→=(x;y-3;z-1)

Theo bài ra, CM→=2MB→

⇒M(-1;4;2)

A(2; 0; 0)

⇒AM=√29

Bài 7: Trong không gian với hệ trục tọa độ Oxyz cho OM→=i→-2j→+3k→, khi đó tọa độ của điểm M với hệ Oxyz là:

   A. (-1;2;-3)    B. (1;-2;3)

   C. (1;-2;1)    D. (-2;1;3)

Lời giải:

Đáp án : B

Bài 8:Trong không gian với hệ toạ độ Oxyz, cho hình bình hành OABD có OA→=a→(-1;1;0), OB→=b→(1;1;0) (O là gốc toạ độ) . Toạ độ tâm hình bình hành OABD là:

   A. (1/2;1/2;0)   B. (1;0;0)

   C. (1;0;1)    D. (1;1;0)

Lời giải:

Đáp án : A

Giải thích :

Tâm hình bình hành OABD là trung điểm của đường chéo OB

⇒Tọa độ tâm là (1/2; 1/2;0)

Bài 9: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-1), B(2;-1;3), C(-2;3;3). Điểm M(a;b;c) là đỉnh thứ tư của hình bình hành ABCM, khi đó P=a²+b²-c² có giá trị bằng:

   A. 44    B. 43

   C. 42    D. 45

Lời giải:

Đáp án : A

Giải thích :

M(a; b; c) ⇒MC→=(-2-a;3-b;3-c)

AB→=(1; -3;4)

ABCM là hình bình hành ⇔AB→=MC→

⇒P=a²+b²-c²=44

Bài 10: Trong không gian với hệ toạ độ Oxyz, có hai điểm trên trục hoành mà khoảng cách từ đó đến điểm M(-3; 4; 8) bằng 12. Tổng hai hoành độ của chúng là:

   A. -6    B. 5

   C. 6    D. 11

Lời giải:

Đáp án : A

Giải thích :

Điểm cần tìm N (x; 0; 0)

MN²=(x+3)²+4²+8²=(x+3)²+80

Theo bài ra: MN = 12

⇒(x+3)²+80=12²⇔(x+3)²=64

⇒ Có 2 điểm N thỏa mãn có tọa độ là (5; 0; 0) và (-11; 0; 0)

⇒Tổng hoành độ của chúng bằng -6

Bài 11: Trong không gian với hệ trục tọa độ Oxyz cho ba điểm A(1;2;-1), B(2;-1;3), C(-2;3;3). Tìm tọa độ điểm D và chân đường phân giác trong góc A của tam giác ABC:

   A. D(0;1;3)    B. D(0;3;1)

   C. D(0;-3;1)   D. D(0;3;-1)

Lời giải:

Đáp án : A

Giải thích :

AB=|AB→ |=√26; AC=|AC→ |=26

AB = AC nên tam giác ABC cân tại A

Do đó điểm D chân đường phân giác trong của góc A là trung điểm của BC

⇒D(0;1;3)

Bài 12: Trong không gian Oxyz cho vecto u→=mi→+j→+2k→. Biết |u→|=√5. Khi đó giá trị m bằng:

   A. m=0    B. m=1

   C. m=2    D. m=-1

Lời giải:

Đáp án : A

Giải thích :

u→=(m;1;2)⇒|u→ |=√(m²+1+2² )=√(m²+5)

Theo bài ra: |u→ |=√5⇒√(m²+5)=√5⇒m=0

Bài 13: Trong không gian Oxyz cho các vectơ a→=(2;1;1), c→=(3;-1;2). Tìm tọa độ của vectơ b→ thỏa mãn biểu thức 2b→-a→+3c→=0→ là:

Lời giải:

Đáp án : C

Giải thích :

2b→-a→+3c→=0→⇒2b→=a→-3c→=(-7;4; -5)

⇒b→=((-7)/2;2; (-5)/2)

Bài 14: Cho hai điểm A(3;4;2) và B(-1;-2;2). Xét điểm C sao cho điểm G(1;1;2) là trọng tâm của tam giác ABC. Chọn câu đúng:

   A. C(1;1;2)    B. C(0;1;2)

   C. C(1;1;0)    D. Không có điểm C như thế.

Lời giải:

Đáp án : A

Giải thích :

C(x; y; z)

G(1; 1; 2) là trọng tâm của tam giác ABC

⇒C(1;1;2)

Bài 15: Chọn hệ tọa độ sao cho các đỉnh A, B, A', C' của hình lập phương ABCD.A'B'C'D' là A(-2; 0; 0), B(1; 0; 0), A’ (0; 0; 1), C’ (1; 1; 1). Tìm tọa độ của tâm hình vuông BCC'B'.

   A. (1/2;1;1)    B.(1;1/2;1)

   C. (1;1/2;1/2)    D. (1;1;1/2)

Lời giải:

Đáp án : C

Giải thích :

Tâm của hình vuông BCC’B’ là trung điểm của đường chéo BC’

⇒Tọa độ tâm là (1;1/2; 1/2 )

Bài tập Tìm tọa độ của vecto, của điểm (P2)

Bài 16: Trong không gian cho hai điểm A(-1;2;3), B(0;1;1), độ dài đoạn bằng:

   A. √6    B. √8

   C. √10    D. √12

Lời giải:

Đáp án : A

Giải thích :

Bài 17: Trong không gian Oxyz, gọi i→, j→, k→là các vectơ đơn vị, khi đó với M(x;y;z) thì OM→bằng:

Lời giải:

Đáp án : A

Giải thích :

Bài 18: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0). Biết tâm đường tròn ngoại tiếp tam giác ABC nằm trong mặt phẳng Oxz, tính bán kính:

Lời giải:

Đáp án : D

Giải thích :

Gọi I (a; 0; c ) là tâm đường tròn ngoại tiếp tam giác ABC

Ta có: IA²=(a-2)²+1²+(c-6)²

IB²=(a+3)²+1²+(c+4)²

IC²=(a-5)²+1²+c²

Do I là tâm đường tròn ngoại tiếp tam giác ABC nên IA = IB = IC hay

IA²=IB²=IC²

Bài 19: Trong không gian với hệ toạ độ Oxyz, cho điểm K(2;4;6), gọi K' là hình chiếu vuông góc của K trên trục Oz, khi đó trung điểm OK' có toạ độ là:

   A. (1;0;0)    B. (0;0;3)

   C. (0;2;0)    D. (1;2;3)

Lời giải:

Đáp án : B

Giải thích :

K’ là hình chiếu vuông góc của K trên trục Oz ⇒K' (0;0;6)

⇒ Trung điểm OK’ có tọa độ là (0; 0; 3)

Bài 20: Trong không gian Oxyz, cho điểm M nằm trên mặt phẳng (Oxy) sao cho M không trùng với gốc tọa độ và không nằm trên hai trục Ox, Oy, khi đó tọa độ điểm M là (a, b, c ≠ 0 ):

   A. (0;b;a)    B. (a;b;0)

   C. (0;0;c)    D. (a;1;1)

Lời giải:

Đáp án : B

Bài 21: Trong không gian với hệ toạ độ Oxyz, cho a→(0;3;4) và |b→|=2|a→|, khi đó tọa độ vectơ b→ có thể là:

   A. (-8;0;-6)    B. (4;0;3)

   C.(2;0;1)    D. (0;3;4)

Lời giải:

Đáp án : A

Giải thích :

|a→ |=5⇒ |b→ |=2|a→ |=10

⇒ b→(-8;0; -6)

Bài 22: Trong không gian với hệ toạ độ Oxyz, cho ba vectơ a→(1;-1;2), b→(3;0;-1), c→(-2;5;1), vectơ m→=a→+ b→- c→có tọa độ là:

   A. (6;0;-6)    B. (-6;6;0)

   C. (6;-6;0)    D. (0;6;-6)

Lời giải:

Đáp án : C

Bài 23: Trong không gian Oxyz cho ba điểm A(1;0;-3), B(2;4;-1), C(2;-2;0). Độ dài các cạnh AB, AC, BC của tam giác ABC lần lượt là:

Lời giải:

Đáp án :A

Bài 24: Trong không gian Oxyz cho ba điểm A(1;0;-3), B(2;4;-1), C(2;-2;0). Tọa độ trọng tâm G của tam giác ABC là:

Lời giải:

Đáp án : B

Bài 25: Trong không gian Oxyz, cho ba vecto a→=(1;2;3), b→=(-2;0;1), c→=(-1;0;1). Tìm tọa độ của vectơ n→=a→+b→+2c→-3i→

   A. n→=(-6;2;-6)    B. n→=(6;2;-6)

    C.n→=(-6;-2;-6)     D.n→=(-6;2;6)

Lời giải:

Đáp án : D

Bài 26: Cho điểm M(1;2;-3), hình chiếu vuông góc của điểm M trên mặt phẳng(Oxy) là điểm:

   A. M'(1;2;0)    B. M'(1;0;-3)

   C. M'(0;2;-3)    D. M'(1;2;3)

Lời giải:

Đáp án : A

Bài 27: Cho điểm M(-2;5;0), hình chiếu vuông góc của điểm M trên trục Oy là điểm

   A. M'(0;-5;0)    B. M'(0;5;0)

   C. M'(2;5;0)    D. M'(-2;0;0)

Lời giải:

Đáp án : B

Bài 28: Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;2). Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là

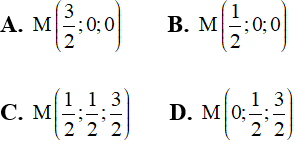
Lời giải:

Đáp án : A

Giải thích :

Theo bài ra, M cách đều 2 điểm A, B

⇔|x-1|=|x-2|⇔x=3/2

⇒M(3/2;0;0)

Bài 29: Trong không gian Oxyz, cho tứ diện ABCD có A(1;0;2), B(-2;1;3), C(3;2;4), D(6;9;-5). Tìm tọa độ trọng tâm G của tứ diện ABCD

   A. G(3;3;14/4)    B. G(8;12;4)

   C. G(2;3;1)    D. G(-9;18/4;-30)

Lời giải:

Đáp án : C

Bài 30: Cho điểm M(3;2;-1), điểm M'(a;b;c) đối xứng của M qua trục Oy, khi đó a+b+c bằng:

   A. 4    B. 6

   C. 0   D. 2

Lời giải:

Đáp án : C

Giải thích :

H ( 0; 2; 0) là hình chiếu vuông góc của M trên Oy

M’ đối xứng với M qua Oy nên H là trung điểm của MM’

⇒M'(-3;2;1)

Khi đó a + b + c = 0