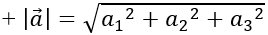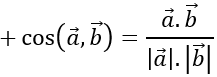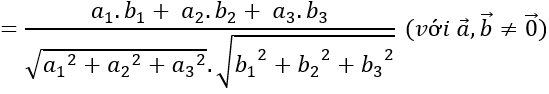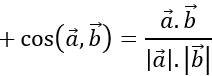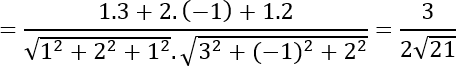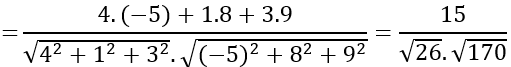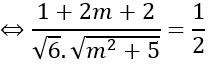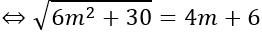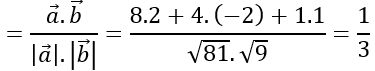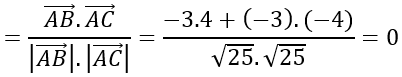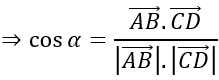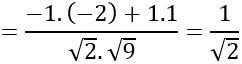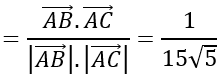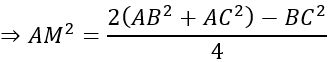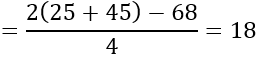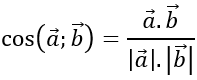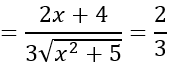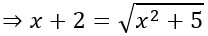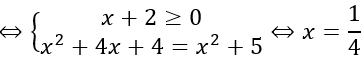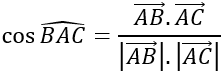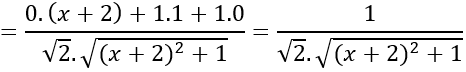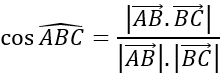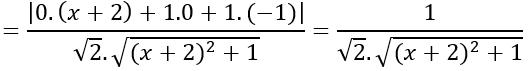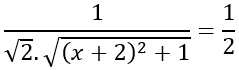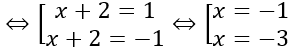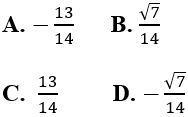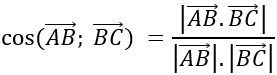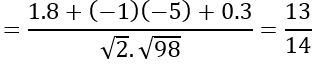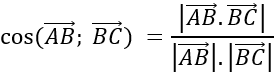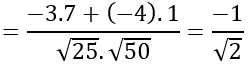Công thức tính Tích vô hướng của hai vecto trong không gian cực hay - Toán lớp 12

---

Công thức tính Tích vô hướng của hai vecto trong không gian cực hay

Với Công thức tính Tích vô hướng của hai vecto trong không gian cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính Tích vô hướng của hai vecto trong không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

+ Tích vô hướng của hai vecto:

    a→.b→=a₁.b₁+ a₂.b₂+ a₃.b₃

+ a→⊥b→⇔a₁.b₁+ a₂.b₂+ a₃.b₃=0

+ a→²=a₁²+a₂²+a₃²

Ví dụ minh họa

Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto a→=(1;2;1),

b→=(3;-1;2), c→=(4; -1; -3),d→=(3; -3; -5),u→=(1;m;2),m∈R.

a) Tính a→.b→; b→(a→-2c→)

b) So sánh a→.(b→.c→) và (a→.b→ ) c→

c) Tính các góc (a→,b→ ), ( a→+b→,3a→- 2c→ )

d) Tìm m để u→⊥(b→+d→)

e) Tìm m để (u→,a→ )=60⁰

Hướng dẫn:

a) a→ =(1;2;1),b→ =(3;-1;2)

⇒a→ .b→ =1.3+2.(-1)+1.2=3.

c→ =(4; -1; -3)⇒2c→ =(8; -2; -6)⇒ a→ -2c→ =(-7;4;7)

⇒b→ (a→ -2c→ )=3.(-7)-1.4+2.7=-11

b) b→ .c→ =3.4+(-1).(-1)+2.(-3)=7⇒a→ .(b→ .c→ )=(7;14;7)

a→ .b→ =3⇒(a→ .b→ ) c→ =(12; -3; -9)

Vậy a→ .(b→ .c→ )≠(a→ .b→ ) c→

c) Ta có:

⇒(a→.b→ )≈71⁰

+ a→+ b→=(4;1;3),3a→- 2c→=(-5;8;9)

⇒cos( a→+b→,3a→- 2c→ )

⇒( a→ +b→ ,3a→ - 2c→ )≈77⁰

d) b→ +d→ =(6; -4; -3); u→ =(1;m;2)

u ⃗⊥(b→ +d ⃗ )⇔u→ .(b→ +d→ )=0⇔6-4m-6=0⇔m=0

e)

(u→ ,a→ )=60⁰⇔cos⁡(u→ ,a→ )=1/2

Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai vecto a→,b→ sao cho (a→,b→ )=120⁰,

|a→ |=2; |b→ |=3. Tính |a→+ b→ | và |a→-2b→ |

Hướng dẫn:

Áp dụng công thức: a→ .b→ =|a→ |.|b→ |.cos⁡(a→ ,b→ )

Ta có: |a→ + b→ |²=(a→ + b→ )²=a→ ²+2a→ .b→ +b→ ²

=|a→ |²+|b→ |²+2|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+9+2.2.3.((-1)/2)=7

⇒|a→ + b→ |=√7

Tương tự:

|a→ -2b→ |² =|a→ |²+4|b→ |²-4|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+36-4.2.3.((-1)/2)=52

⇒|a→ -2b→ |=2√(13)

Bài 3: Trong không gian Oxyz, cho các điểm A(2; -1; 1), B(3; 5; 2), C(8; 4; 3), D(-2; 2m+1; -3)

a) Chứng minh tam giác ABC là tam giác vuông

b) Tìm m sao cho tam giác ABD vuông tại A

c) Tính số đo góc A của tam giác ABC

Hướng dẫn:

a) Ta có: AB→=(1;6;1); BC→=(5;-1;1)

⇒AB→.BC→=1.5+6.(-1)+1.1=0

⇒AB→⊥BC→⇒ΔABC vuông tại B.

b) AB→=(1;6;1); AD→=(-4;2m+2; -4)

Tam giác ABD vuông tại A ⇔AB→.AD→=0

⇔1.(-4)+6.(2m+2)+1.(-4)=0

⇔12m+4=0⇔m=(-1)/3

c) AB→=(1;6;1); AC→=(6;5;2)

cos⁡A=cos⁡(AB→;AC→ )

⇒Â≈40⁰

B. Bài tập vận dụng

Bài 1: Cho các vectơ u→(u₁;u₂;u₃) và v→(v₁;v₂;v₃), u→. v→=0 khi và chỉ khi:

   A. u₁v₁+u₂v₂+u₃v₃=0

   B. u₁+v₁+u₂+v₂+u₃+v₃=0

   C. u₁v₁+u₂v₂+u₃v₃=1

   D. u₁v₂+u₂v₃+u₃v₁=-1

Lời giải:

Đáp án : A

Bài 2: Cho hai vectơ a→ và b→ tạo với nhau góc 60⁰ và |a→| =2; |b→| =4. Khi đó |a→ + b→ | bằng:

   A. 2√7    B. 2√3

   C. 2√5   D. 2

Lời giải:

Đáp án : A

Giải thích :

|a→ + b→ |²=(a→ + b→ )²=|a→ |²+|b→ |²+2|a→ |.|b→ |.cos⁡(a→ + b→ )

=4+16+2.2.4.1/2=28

⇒|a→ + b→ |=2√7

Bài 3: Cho a→(-2;1;3), b→(1;2;m). Với giá trị nào của m để a→ vuông góc với b→ ?

   A. m=-1   B. m=1

   C. m=2   D. m=0

Lời giải:

Đáp án : D

Giải thích :

a→ vuông góc với b→ khi và chỉ khi a→ . b→=0

⇔-2.1+1.2+3.m=0⇔m=0

Bài 4: Tính cosin của góc giữa hai vectơ a→ và b→ biết a→(8;4;1), b→(2;-2;1)

   A. 1/2   B. √(2)/2

   C. √(3)/2   D. 1/3

Lời giải:

Đáp án : D

Giải thích :

cos⁡(a→ , b→)

Bài 5: Cho tam giác ABC với A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Khi đó số đo của góc BACˆ bằng:

   A. 30⁰    B. 90⁰

   C. 60⁰   D. 45⁰

Lời giải:

Đáp án : B

Giải thích :

AB→=(-3;0; -4); AC→=(4;0;-3)

cos⁡BACˆ=cos⁡( AB→ ; AC→)

⇒BACˆ=90⁰

Bài 6: Cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Khi đó số đo của góc giữa hai đường thẳng AB và CD là :

   A. 30⁰    B. 45⁰

   C. 60⁰   D. 90⁰

Lời giải:

Đáp án : B

Giải thích :

AB→ =(-1;1;0); CD→ =(-2;1; -2)

Gọi góc giữa 2 đường thẳng AB và CD là α

⇒α=45⁰

Bài 7: Trong không gian với hệ toạ độ Oxyz, cho hai vecto a→; b→. Trong các khẳng định sau, khẳng định nào đúng:

   A. a→ .|b→ |=|a→ |.b→ với mọi a→ ; b→

   B. ( a→ b→ )²=a→ ² . b→ ² với mọi a→ ; b→

   C. |a→ . b→ | ≤|a→ |.|b→ | với mọi a→ ; b→

   D. a→ . b→ =0 khi và chỉ khi a→ = 0→ hoặc b→ = 0→

Lời giải:

Đáp án : C

Giải thích :

VD: a→ =(2; -3;1), b→ =(1;1;1)

⇒|a→ |=√14; |b→ |=√3

a) a→ . |b→ |=(2√3; -3√3;√3)

|a→ |. b→ =(√14; √14; √14)

⇒ a→ . |b→ |≠| a→ | . b→

b) a→ b→ =2.1-3.1+1.1=0

a→ ² . b→ ²=14.3=52

⇒( a→ b→ )²≠ a→ ² . b→ ²

d) a→ b→ =0 nhưng a→ ≠ 0→ hoặc b→ ≠ 0→

Vậy a, b, d sai, c đúng.

Bài 8: Trong không gian Oxyz, cho a→(-1;2;-3), b→(3;3;4), c→(5;0-1). Giá trị của a→ (b→ + c→ ) là:

   A. 8   B. 11

   C. -8   D. -11

Lời giải:

Đáp án : D

Giải thích :

b→ + c→ =(8;3;3)

⇒ a→ (b→ + c→ )=-1.8+2.3-3.3=-11

Bài 9: Cho 3 điểm A(2; 1; -3), B(–2; 2; –6), C(5; 0; –1). Tích AB→. AC→ bằng:

   A. -6   B. 65

   C. -19    D. 33

Lời giải:

Đáp án : C

Giải thích :

AB→ =(-4;1; -3); AC→=(3; -1;2)

⇒ AB→ . AC→ =-4.3+1.(-1)-3.2=-19

Bài 10: Trong không gian với hệ tọa độ Oxyz, điều kiện để a→ vuông góc với b→ là gì ?

   A. a→ . b→ =0   B. [ a→ , b→] = 0→

   C. a→ + b→ = 0→   D. a→ - b→ = 0→

Lời giải:

Đáp án : A

Giải thích :

Bài 11: Cho hai vecto a→; b→thay đổi nhưng luôn thỏa mãn |a→|=5; |b→ |=3. Giá trị lớn nhất của |a→ -2 b→ | là:

   A. 11   B. -1

   C. 1    D. √61

Lời giải:

Đáp án : D

Giải thích :

Ta có: |a→ - 2 b→ |² = ( a→ - 2 b→ )² = | a→ |² + 4| b→ |² - 4| a→ |.| b→ |.cos⁡( a→ ; b→ )

| a→ -2 b→ | lớn nhất ⇔ | a→ - 2 b→ |² lớn nhất ⇔cos⁡( a→ ; b→ )=0

Khi đó: | a→ - 2 b→ |²=| a→ |²+4| b→ |²=25+4.9=61

⇒|a→ - 2 b→ |=√61

Bài 12: Trong không gian với hệ toạ độ Oxyz, cho ba vectơ a→(-1;1;0), b→(1;1;0), c→(1;1;1,). Trong các mệnh đề sau, mệnh đề nào sai ?

   A. | a→|= √2    B. c→ ⊥ b→

   C. a→ ⊥ b→   D. | c→ |=√3

Lời giải:

Đáp án : B

Giải thích :

Ta có: c→ . b→=1.1+1.1+0.1=2≠0

⇒ Hai vecto c→ ; b→ không vuông góc với nhau

Bài 13: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có AB→=(-3;0;4), AC→=(5;-2;4). Độ dài trung tuyến AM là:

   A. 3√2   B. 4√2

   C. 2√3   D. 5√3

Lời giải:

Đáp án : A

Giải thích :

Ta có: AB=|AB→ |=5; AC=|AC→ |=√45

cos⁡BACˆ =cos⁡(AB→ ; AC→ )

Ta có: BC²=AB²+AC² - 2AB.AC.cos⁡BACˆ =68

AM là trung tuyến

⇒AM=3√2

Bài 14: Cho | a→ |=2; | b→ |=5, góc giữa hai vectơ a→ và b→ bằng (2π)/3, u→ = k a→ - b→; v→ = a→ + 2 b→. Để u→ vuông góc với v→ thì k bằng?

   A. -45/6   B. 45/6

   C. 6/45   D. -6/45

Lời giải:

Đáp án : A

Giải thích :

u→ = k a→ - b→; v→ = a→ + 2 b→

⇒ u→ . v→ =(k a→ - b→ )(a→ +2 b→ )=k a→ ²-2 b→ ²+(2k-1) a→ . b→

Ta có: a→ . b→ =| a→ |.| b→ |.cos⁡( a→ ; b→ )=2.5.cos⁡(2π/3)=-5

⇒ u→ . v→ =4k-2.25+(2k-1).(-5)=-6k-45

Giả thiết: u→ và v→ vuông góc với nhau ⇒ u→ . v→ =0

⇒-6k-45=0 ⇔ k=(-45)/6

Bài 15: Trong không gian với hệ tọa độ Oxyz, cho a→=(x;2;1), b→ =(2;1;2), Tìm x biết cos( a→ , b→ )=2/3.

   A. x=1/2   B. x=1/3

   C. x=3/2   D. x=1/4

Lời giải:

Đáp án : D

Giải thích :

Bài 16: Trong không gian với hệ tọa độ Oxyz, cho A→ (-2;2;-1), B→ (-2;3;0), C→ (x;3;-1). Giá trị của x để tam giác ABC đều là:

   A. x=-1   B. x=-3

   C.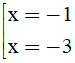   D. x=1

Lời giải:

Đáp án : C

Giải thích :

AB→ =(0;1;1); AC→ =(x+2;1;0); BC→ =(x+2;0;-1)

Tam giác ABC đều ⇔ BACˆ= ABCˆ=60⁰

Khi đó:

⇔(x+2)² + 1=2⇔(x+2)²=1

Bài 17: Cho hai vecto a→; b→ tạo với nhau một góc 60⁰. Biết độ dài của hai vecto đó lần lượt là 5 và 10. Độ dài của vecto hiệu a→ - b→ là:

   A. 15   B. 5

   C. 75   D. √(75)

Lời giải:

Đáp án : D

Giải thích :

Ta có: | a→ - b→ |²=( a→ - b→ )²=| a→ |²+| b→ |²-2| a→ |.| b→ |.cos⁡( a→ ; b→ )

=25+100-2.5.10.cos⁡60⁰ =75

⇒|a→ - b→ |=√75

Bài 18: Trong không gian với hệ tọa độ Oxyz,cho tam giác ABC với A(-4;3;5), B(-3;2;5) và C(5;-3;8). Tính cos⁡(AB→ ; BC→ ).

Lời giải:

Đáp án : C

Giải thích :

AB→ =(1; -1;0); BC→ =(8; -5;3)

Bài 19: Trong không gian với hệ toạ độ Oxyz, tam giác ABC có A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Số đo của góc B là:

   A. 45⁰   B. 60⁰

   C. 30⁰   D. 120⁰

Lời giải:

Đáp án : A

Giải thích :

AB→=(-3; 0;-4); BC→=(7; 0;1)

⇒(AB→ ; BC→ )=135⁰

⇒ Bˆ=45⁰

Bài 20: Trong không gian Oxyz, cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn điều kiện x²+y²+z²=4; m²+n²+p²=9. Vecto AB→ có độ dài nhỏ nhất là:

   A. 5   B. 1

   C. 13   D. Không tồn tại

Lời giải:

Đáp án : B

Giải thích :

Ta có: OA = 2; OB = 3

AB≤|OA-OB|=1

Dấu bằng xảy ra khi O nằm ngoài đoạn AB.