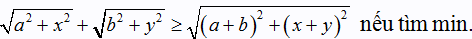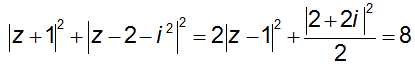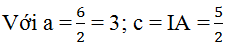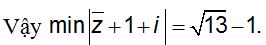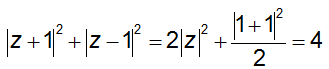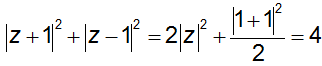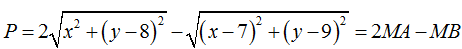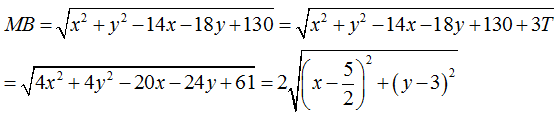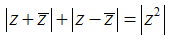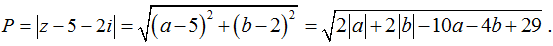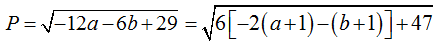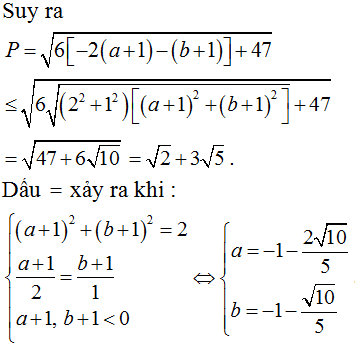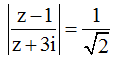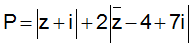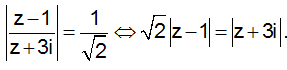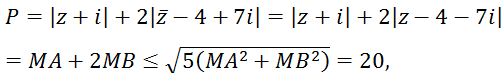Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2) - Toán lớp 12

Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2)

Với Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 2) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm giá trị nhỏ nhất, lớn nhất của số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Cho |z + a| = |z + b| Tìm Max, min P với P = |z + z₁| + |z + z₂|

1. Phương pháp

Cách 1:

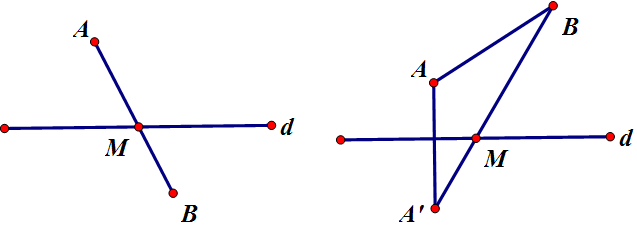
+) Bước 1: Khai triển |z + a| = |z + b| đưa về dạng đường thẳng

+) Bước 2 : Từ P ta tìm tọa độ điểm A ; B và xét vị trí tương đối của A ;B với d

+) Khi đó z là M thỏa mãn P min :

Cách 2:

Áp dụng

BĐT Bunhia Copski: (Ax + By)² ≤ (A² + B²)(x² + y²) nếu tìm max

BĐT Mincopxki:

2. Ví dụ minh họa

Ví dụ 1: Cho số phức z thỏa mãn điều kiện |z - 1| = √2. Tìm giá trị lớn nhất của T = |z + i|+ |z - 2 - i|

A. maxT = 8√2    B. maxT = 4    C. maxT = 4√2    D. maxT = 8

Hướng dẫn:

Áp dụng công thức độ dài đường trung tuyến ta có:

Theo bất đẳng thức Bunhiacopxki thì

T² ≤ (|z + 1|² + |z - 1|²)(1²+ 1²) = 16 => T ≤ 4

Chọn đáp án là B.

Ví dụ 2: Cho |z - i| + |z - 3 + 3i| = 6. Tính max min của P = |z - 6 + 7i|

Hướng dẫn:

Cách 1: PP hình học

Nhắc lại: Gọi A và B là điểm biểu diễn z₁; z₂ và M là điểm biểu diễn z; C là điểm biểu diễn z₃ trong P

Khi đó MA + MB = k

Nếu MA+ = AB thì điểm biểu diễn là đường thẳng

Nếu MA + MB > AB thì điểm biểu diễn là elip

Khi đó ta vẽ hình biểu diễn các điểm A, B, C trên mặt Oxy và xác định M trong các trường hợp là đường thẳng hoặc elip sao cho MC ngắn nhất hoặc lớn nhất.

Lời giải

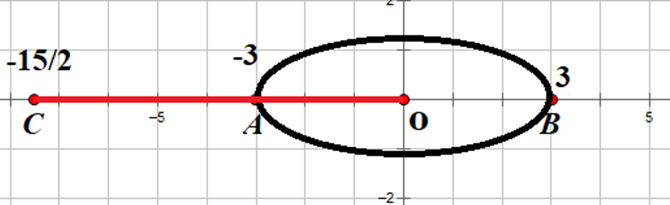
Gọi A(0; 1);B(3; -3);C(6; -7);M(x; y)

Khi đó MA + MB = 6; Tìm max min của MC

Ta thấy MA + MB > AB => Elip Trong đó I là trung điểm AB

Khi đó

MC min khi MC = B’C = BC - BB’ = BC - (a - c) = 5 - (1/2) = 4,5

MC max khi MC = A’C = AC + AA’ = AC + (a - c) = 10 + (1/2) = 10,5

Cách 2: Dùng máy tính CASIO

Ví dụ 3: Cho số phức z thỏa mãn |z - 2 - 3i| = 1. Giá trị nhỏ nhất của |z + 1 + i| là:

A. √13 - 1    B. 4    C. -4    D. √13 + 1

Hướng dẫn:

Ta có:

|z + 1 + i| = |z + 1 -i| = |(z - 2 - 3i) + (3 + 2i)| ≥ ||z - 2 - 3i| - |3 + 2i|| = √13 - 1

Chọn đáp án là A.

Ví dụ 4: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức T = |z + 1| + 2|z - 1|

A. max T = 2√5    B. max T = 2√10    C. max T = 3√5    D. max T = 3√2

Hướng dẫn:

Áp dụng công thức độ dài đường trung tuyến ta có:

Theo bất đẳng thức Bunhiacopxki thì:

T² ≤ (|z + 1|² |z - 1|²)(1² + 2²) = 20 => T ≤ 2√5

Chọn đáp án là A.

Ví dụ 5: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức: T = |z + 1| + 3|z - 1|

A. max T = 3√10    B. max T = 2√10     C. max T = 6    D. max T = 4√2

Hướng dẫn:

Áp dụng công thức trung tuyến ta có :

Theo bất đẳng thức Bunhiacopxki thì

T² ≤ (|z + 1|² + |z - 1|²)(1² + 3²) = 40 => T ≤ 2√10

Chọn đáp án là B.

Ví dụ 6: Cho số phức z thay đổi và thỏa mãn |z - 1 - i| = 5. Tìm giá trị lớn nhất của biểu thức P = 2|z - 8i| - |z - 7 - 9i| bằng:

Hướng dẫn:

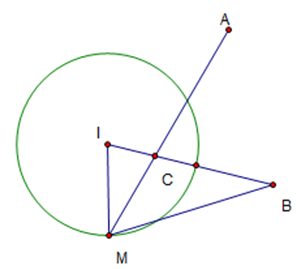
Gọi M(x; y) biểu diễn số phức z, từ |z - 1 - i| = 5 thì M nằm trên đường tròn (x - 1)² + (y - 1)² = 25 có tâm và bán kính : I(1; 1), R = 5.

Gọi A(0; 8); B(7; 9) thì:

Phân tích : mục tiêu tìm tọa độ điểm sao cho MB = 2MC, nhận thấy IB = 2IM = 2R nên ta có hai cách tìm tọa độ điểm C như sau :

Cách 1 : (x - 1)² + (y - 1)² = 25 ⇔ T = x² + y² - 23 = 0

Nên chọn điểm 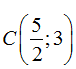thì MB = 2MC

Cách 2 : Lấy điểm C thỏa mãn 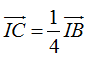thì tam giác IMC đồng dạng với tam giác IMB nên ta có MB = 2MC từ đó

Ta có: P = 2MA - MB = 2(MA - MC) ≤ 2Ac = 5√5

Dấu "=" đạt được khi điểm C nằm trên đoạn AM.

Chọn B.

Ví dụ 7: Cho số phức z thoả mãn:

Giá trị lớn nhất của biểu thức: P = |z - 5 - 2i| bằng

A. √2 + 5√3     B. √2 + 3√5

C. √5 + 2√3     D. √5 + 3√2

Hướng dẫn:

Cách 1: Đại số

Đặt z = a + bi

Từ giả thiết:

⇔ 2|a| + 2|b| = a² + b²

⇔ (|a| - 1)² + (|b| - 1)² = 2 (1)

Ta có:

Dễ thấy P lớn nhất khi a, b ≤ 0. Khi đó:

Do a, b ≤ 0 nên từ (1) ta có: (a + 1)² + (b + 1)² = 2

Chọn B.

Cách 2: Hình học

Đặt z = a + bi.

Từ giả thiết

⇔ 2|a| + 2|b| = a² + b²

⇔ (|a| - 1)² + (|b| - 1)² = 2 (1)

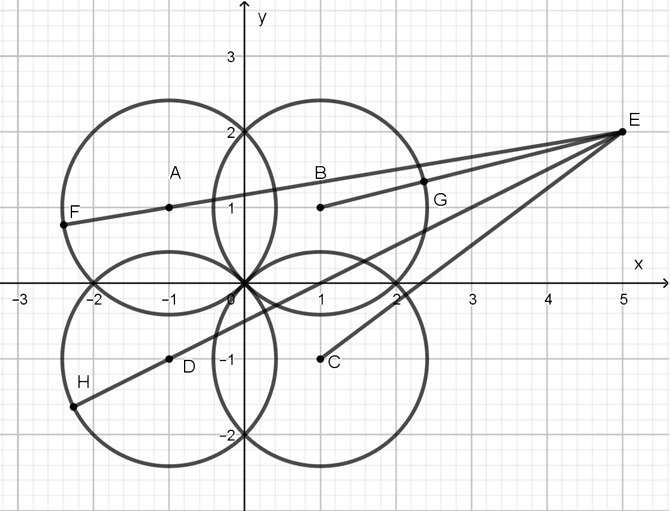
Tập hợp M biểu diễn z thuộc các phần đường tròn cùng bán kính là R = √2 có tâm là A(-1; 1), B(1; 1), C(1; -1), D(-1; -1) nằm chọn vẹn trong 1 góc phần tư (bỏ đi các cung nhỏ).

P = ME với E(5; 2). Từ hình vẽ ta thấy max P = HE = ED + √2 = 3√5 + √2

Ví dụ 8: Cho số phức z thỏa mãn

Tìm giá trị lớn nhất của biểu thức:

A. 10     B. 20    C. 2√5    D. 4√5

Hướng dẫn:

Ta có:

Gọi M là điểm biểu diễn số phức, tập hợp điểm biểu diễn số phức z là đường tròn có phương trình:

(x - 2)² + (y - 3)² = 20 (C)

= |z + i| + 2|z - 4 - 7i|, A(0; -1); B(4; 7) lần lượt biểu diễn 2 số phức z₁ = -i, z₂ = 4 + 7i. Ta có A, B ∈ (C), AB = 4√5 = 2R nên nên AB là bán kính đường tròn (C)=> MA² + MB² = AB² = 80

Mặt khác:

dấu “=” xảy ra khi MB = 2MA

Vậy maxP = 20

Chọn B.