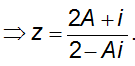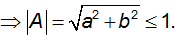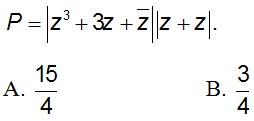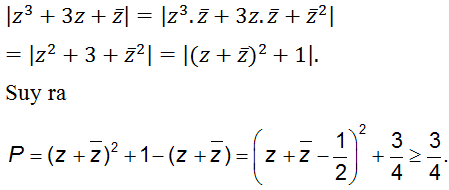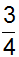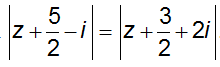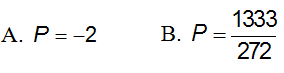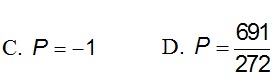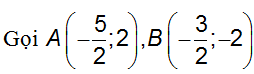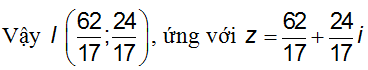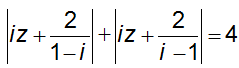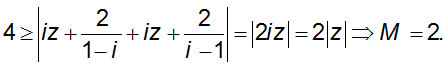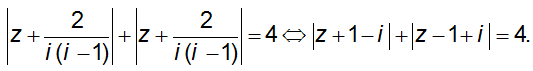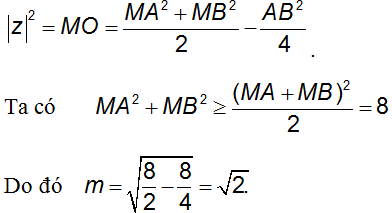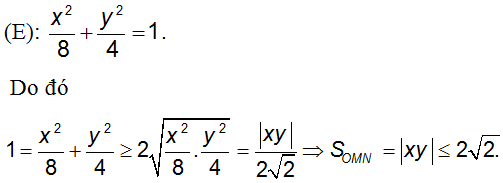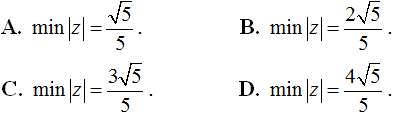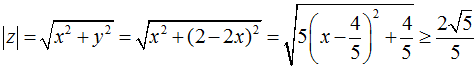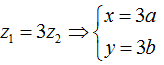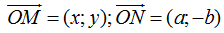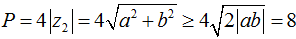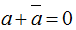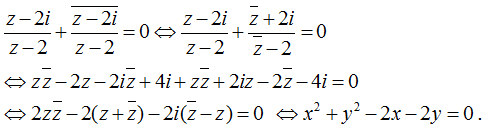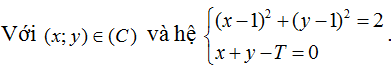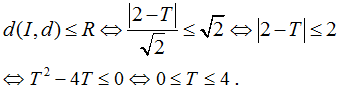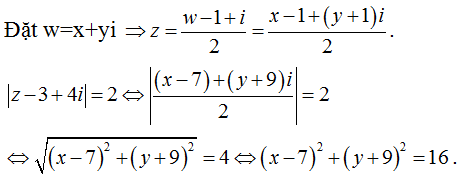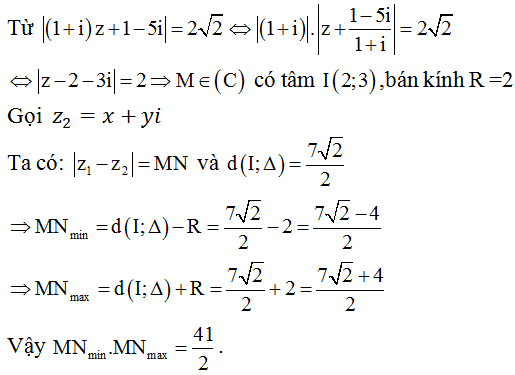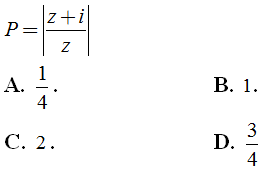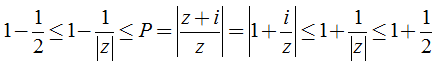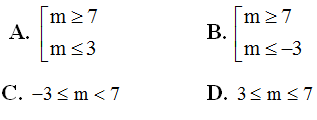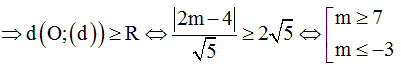Tìm giá trị nhỏ nhất, lớn nhất của số phức (tổng hợp) - Toán lớp 12
Tìm giá trị nhỏ nhất, lớn nhất của số phức (tổng hợp)
Với Tìm giá trị nhỏ nhất, lớn nhất của số phức (tổng hợp) Toán lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm giá trị nhỏ nhất, lớn nhất của số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
Câu 1: Cho số phức z thỏa mãn |z| ≤ 1. Đặt A =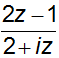 
. Mệnh đề nào dưới đây đúng?
A. |A| < 1 B. |A| ≤ 1 C. |A| ≥ 1 D. |A| > 1
Hướng dẫn:
Ta có:
2A + Aiz = 2z - i ⇔ (2 - Ai)z = 2A + i
Đặt A = a + bi.
Suy ra
|z| ≤ 1 ⇒ |2A + i| ≤ |2 - Ai| ⇔ 4a2 + (2b + 1)2 ≤ a2 + (b + 2)2 ⇔ 3a2 + 3b2 ≤ 3
Chọn đáp án là B.
Câu 2: Cho số phức z thỏa mãn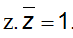 
. Tìm giá trị nhỏ nhất của biểu thức :
Hướng dẫn:
Ta có:
Vậy giá trị nhỏ nhất của P là 
Chọn đáp án C.
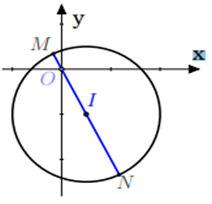
Câu 3: Cho số phức z thỏa mãn |z - 1| 2i| = 3. Mô đun lớn nhất của số phức z là:
A. 3 + √5 B. 2√5 C. 3 D. Tất cả sai
Hướng dẫn:
Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm I(1; −2) bán kính r = 3. Khi đó |z| = OM với O là gốc tọa độ. Do đó
max |z| = OI + r = 3 + √5
Chọn đáp án là A.
Câu 4: Cho số phức z, w thỏa mãn |z - 1 + 2i| = |z + 5i|, w = iz + 20. Giá trị nhỏ nhất m của |w| là
Hướng dẫn:
Gọi A (1; −2), B (0; −5), tập hợp các điểm z thỏa mãn giả thiêt đề bài là đường trung trực d của AB có phương trình x + 3y + 10 = 0. Ta có |w| = |iz + 20| = |z - 20i| = OM với M là điểm biểu diễn số phức z và C(0; 20). Do đó min |w| = d(C.∆) = 7√10
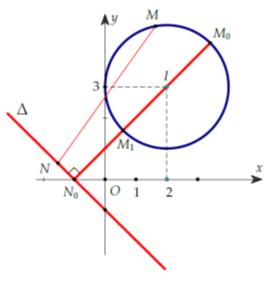
Câu 5: Cho số phức z thỏa mãn:
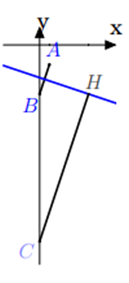
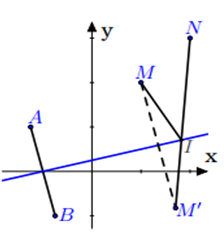
Biết biểu thức Q = |z - 2 - 4i| + |z - 4 - 6i| đạt giá trị nhỏ nhất tại z = a + bi (a, b ∈ R). Tính P = a − 4b
Hướng dẫn:
tập hợp các điểm z thỏa mãn giả thiêt đề bài là đường trung trực d của AB có phương trình x − 4y + 2 = 0.
Xét hai điểm M(2; 4), N(4; 6) thì Q = IM + IN với I ∈ d.
Do đó Q nhỏ nhất khi và chỉ khi I là giao điểm của M0N với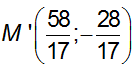 
là điểm đối xứng của M qua d
Chọn đáp án là A.
Câu 6: Cho số phức z thỏa mãn:
Gọi M và m lần lượt là Giá trị lớn nhất và Giá trị nhỏ nhất của |z|. Tính M.m
A. Mnm = 2 B. Mm = 1 C. Mm = 2√2 D. Mm = 2√3
Hướng dẫn:
Ta có:
Theo giả thiết thì số phức z thỏa mãn
Gọi A(−1; 1), B(1; −1) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theo công thức trung tuyến thì
Vậy Mm = 2√2.
Chọn đáp án là C.
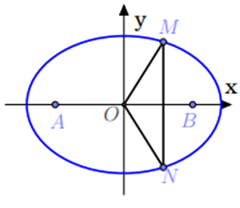
Câu 7: Cho z là số phức thay đổi thỏa mãn |z - 2| + |z + 2| = 4√2. Trong mặt phẳng tọa độ, gọi M, N là điểm biểu diễn z và z. Tính giá trị lớn nhất của diện tích tam giác OMN
A. 1 B. √2 C. 4√2 D. 2√2
Hướng dẫn:
Gọi điểm M biểu diễn số phức z = x + iy và N biểu diễn số phức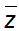 
thì M, N đối xứng nhau qua Ox. Diện tích tam giác OMN là SOMN = |xy|
Do |z - 2| + |z + 2| = 4√2 nên tập hợp M biểu diễn x là Elip
Chọn đáp án là D.
Câu 8: Trong các số phức thỏa mãn điều kiện (z - 1)(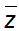 + 2i) là số thực. Tính giá trị nhỏ nhất của mô – đun của số phức z.
Hướng dẫn:
Giả sử z = x + yi,
Khi đó (z - 1)(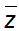 + 2i) = x(x - 1) + y(y - 2) + [xy - (x - 1)(y - 2)]i
theo bài do số phức trên là số thực nên xy - (x - 1)(y - 2) = 0 ⇔ y = 2 - 2x
Từ đó ta có:
Chọn đáp án B.
Câu 9: Cho hai số phức z1, z2 thỏa mãn |z1|z1 = 9|z2|z2 và nếu gọi M, N lần lượt là điểm biểu diễn của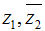 
trong mặt phẳng tọa độ Oxy thì tam giác OMN có diện tích bằng 6. Tính giá trị nhỏ nhất của P = |z1 + z2
A. min P = 8 B. min P = 6
C. min P = 4√2 D. min P = 3√2
Hướng dẫn:
+ Từ |z1|z1 = 9|z2|z2 suy ra |z1| = 3|z2| = 3t (t > 0) và điểm biểu diễn cho số phức z1, z2 và điểm thẳng hàng (các véc tơ còn cùng hướng). Trong đó điểm N' đối xứng của điểm N qua trục Ox là điểm biểu diễn cho số phức z2. Thế vào hệ thức trên ta được:
+ Giả sử z1 = x + yi; z2 = a + bi, (a, b, x, y ∈ R) suy ra M(x; y); N(a; -b); N'(a; b). Ta có:
Từ đó ta có: |bx + ay| = 12 hay |ab| = 2 (1)
Ta có:
Dấu bằng diễn ra khi và chỉ khi
Chọn đáp án A.
Câu 10: Xét tập A gồm các số phức z thỏa
là số thuần ảo và các giá trị m, n thỏa chỉ có duy nhất số phức z ∈ A thỏa |z - m - mi| = √2. Đặt M = max(m + n), N = min(m + n) thì giá trị của tổng M + N là?
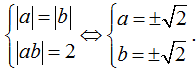
A. -2 B. - 4 C. 2 D. 4
Hướng dẫn:
Vận dụng tính chất ta có a thuần ảo thì
Từ giả thiết suy ra:
Vậy tập hợp A là đường tròn (C) có tâm I(1;1) bán kính R = √2.
Ta có: |z - m - mi| = √2 ⇔ (x - m)2 + (y - n)2 = 2 do phương trình này có nghiệm duy nhất nên x = m, y = n
Vậy ta có: M = max(x + y); m = min(x + y).
Gọi M là một giá trị của x+ y hay x + y = T ⇔ x + y - T = 0
+ Xét đường thẳng d: x + y - T = 0
Hệ trên có nghiệm khi và chỉ khi:
Vậy M = 4; m = 0 nên M + m = 4.
Chọn đáp án D.
Câu 11: Trong mặt phẳng phức Oxy, các số phức z thỏa |z + 2i - 1| = |z + i|. Tìm số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1 ;3) .
A.3 + i B. 1 + 3i. C. 2 - 3i. D. -2 + 3i.
Hướng dẫn:
Gọi M(x ; y) là điểm biểu diễn số phức z = x + yi (x, y ∈ R)
Gọi E(1 ; -2) là điểm biểu diễn số phức 1 - 2i
Gọi F(0 ; -1) là điểm biểu diễn số phức -i
Ta có: |z + 2i - 1| = |z + i| ⇔ ME = MF => Tập hợp điểm biểu diễn số phức z là đường trung trực EF : x - y - 2 = 0.
Để MA ngắn nhất khi MA ⊥ EF tại M ⇔ M(3; 1) => z = 3 + i
Chọn A.
Câu 12: Cho số phức z thoả |z - 3 + 4i| = 2 và w = 2z + 1 - i. Khi đó |w| có giá trị lớn nhất là:
Hướng dẫn:
=> Tập hợp điểm biểu diễn số phức w là đường tròn tâm I(7;-9) bán kính R = 4.
Khi đó |w| có giá trị lớn nhất là OI + R = √130 + 4
Câu 13: Cho số phức z1 thỏa mãn |(1 + i)z + 1 - 5i| = 5√2 và số phức z2 thỏa mãn |z + 1 + 2i| = |z+ i|. Tính tích giá trị lớn nhất và giá trị nhỏ nhất của |z1 - z2|
Hướng dẫn:
Gọi M, N lần lượt là điểm biểu diễn số phức z1; z2 trên mặt phẳng.
Chọn B.
Câu 14: Cho số phức z thỏa mãn |z| ≥ 2. Tính giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
Hướng dẫn:
Áp dụng BĐT ||z2| - |z1|| ≤ |z1 + z2| ≤ |z1| + |2|
Ta có:
Do đó maxP = 3/2; minP = 1/2
MaxP.minP = 3/4
Chọn D.
Câu 15: Cho hai số phức z; w thỏa mãn |z - 1| = |z + 3 - 2i|; w = z + m + i với m ∈ R là tham số. Giá trị của m để ta luôn có |w| ≥ 2√5 là:
Hướng dẫn:
Ta có: z = w - m - i => |w - m - 1 - i| = |w + 3 - m - 3i|
Tập hợp điểm M biểu diễn w là trung trực của A(m + 1; 1); B(m - 3; 3) nên là đường thẳng d qua trung điểm I(m - 1; 2) và có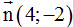 
=> d: 2x - y - 2m + 4 = 0
Đặt z = a + bi do |w| ≥ 2√5 nên M nằm ngoài đường tròn tâm O bán kính R = 2√5
Chọn B.
