Tính thể tích khối lăng trụ đứng biết chiều cao và độ dài cạnh đáy - Toán lớp 12

Tính thể tích khối lăng trụ đứng biết chiều cao và độ dài cạnh đáy

Với Tính thể tích khối lăng trụ đứng biết chiều cao và độ dài cạnh đáy Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính thể tích khối lăng trụ đứng biết chiều cao và độ dài cạnh đáy từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

+ Thể tích khối lăng trụ đứng là: V = S.h

( S là diện tích đáy, h là chiều cao của hình lăng trụ).

2. Ví dụ minh họa

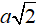
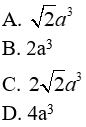
Ví dụ 1. Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác ABC vuông cân tại A có cạnh BC= và biết A'B = 3a. Tính thể tích khối lăng trụ.

Hướng dẫn giải

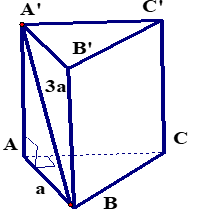
+ Do tam giác ABC là tam giác vuông cân tại A có BC=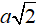 Nên AB= AC= a.

+ Do ABC. A'B'C' là lăng trụ đứng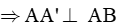

Xét tam giác vuông AA’B ta có:

AA’² = A’B² – AB² = 9a² – a² = 8a²

=>

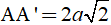
Diện tích tam giác ABC là: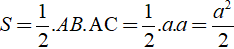

+ Thể tích hình lăng trụ đã cho là: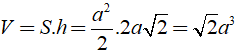

Chọn A.

Ví dụ 2. Cho lăng trụ tứ giác đều ABCD.A’B’C’D' có cạnh bên bằng 4a và đường chéo 5a. Tính thể tích khối lăng trụ này.

A. 6a³

B. 12a³

C. 18a³

D. 24a³

Hướng dẫn giải

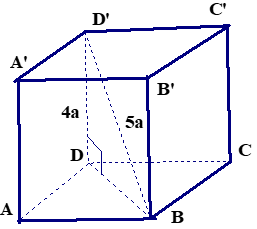
+ Do ABCD. A'B'C'D' là lăng trụ đứng có cạnh bên là 4a nên AA’= BB’= CC’= DD’= 4a . Đường chéo của hình lăng trụ là BD’ = 5a.

+ Tam giác BDD’ vuông tại D nên:

BD² = BD'² - DD'² = 25a² - 16a² = 9a²

=> BD = 3a

+ Tứ giác ABCD là hình vuông nên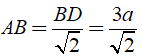

Suy ra, diện tích hình vuông ABCD là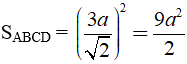

Vậy thể tích hình lăng trụ là: V= S_ABCD. AA’ =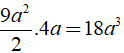

Chọn C.

Ví dụ 3. Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a = 4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ.

Hướng dẫn giải

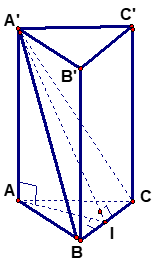
Gọi I là trung điểm BC.

Do tam giác ABC là tam giác đều nên AI= AB. sin B = 4. sin60^o =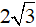 và AI⊥BC

Mà AA'⊥BC nên A'I⊥BC( định lí ba đường vuông góc)

Diện tích tam giác A’BC là:

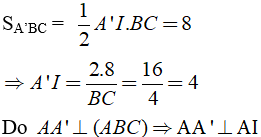
Xét tam giác AA’I vuông tại A ta có:

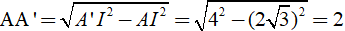
Diện tích tam giác ABC là: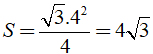

Thể tích hình lăng trụ là: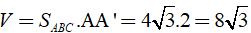

Chọn D.

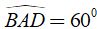
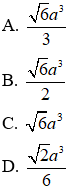
Ví dụ 4. Cho hình hộp đứng có đáy là hình thoi cạnh a và có góc . Đường chéo lớn của đáy bằng đường chéo nhỏ của lăng trụ. Tính thể tích hình hộp .

Hướng dẫn giải

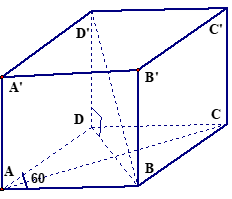
* Tam giác ABD cân tại A( vì AB = AD)

Lại có: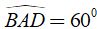 nên tam giác ABD là tam giác đều cạnh a => BD = a

* Diện tích tam giác ABD là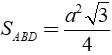

=>

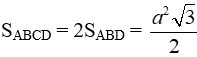
+ Gọi O là giao điểm của AC và BD.

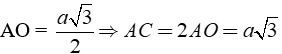
Theo đề bài BD'= AC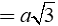

* Xét tam giác vuông BDB’ có:

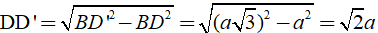
Vậy thể tích của hình hộ đã cho là;

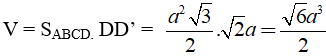
Chọn B.