Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H
Câu hỏi:
Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A, B, C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
A. 2x + y + z - 6 = 0
B. x + 2y + z - 6 = 0
C. x + 2y + 2z - 6 = 0
D. 2x + y + z + 6 = 0
Trả lời:
Chọn A
Cách 1. Giả sử A (a; 0; 0) ∈ Ox, B (0;b;0) ∈ Oy, C (0;0;c) ∈ Oz.
Khi đó mặt phẳng (P) có dạng: 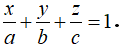
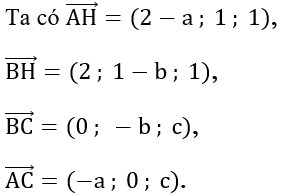
Do H là trực tâm tam giác ABC nên:
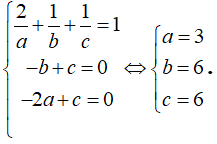
Vậy phương trình của mặt phẳng (P) là:
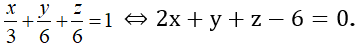
Cách 2. Vì tứ diện OABC có các cạnh đôi một vuông tại O và H là trực tâm tam giác ABC nên 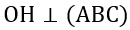 (tham khảo bài tập 4, trang 105 SGK HH11).
(tham khảo bài tập 4, trang 105 SGK HH11).
Suy ra 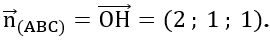 Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
H ∈ (P) nên: 2.2 + 1 + 1 + D = 0 => D = -6
Vậy phương trình mặt phẳng là: 2x + y + z - 6 = 0
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho ba điểm A(0;0;-1), B(-1;1;0), C(1;0;1). Tìm điểm M sao cho 3MA2 + 2MB2 - MC2 đạt giá trị nhỏ nhất.
Xem lời giải »
Câu 3:
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
Xem lời giải »
Câu 4:
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
Xem lời giải »
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 0; -2), B(4; 0; 0). Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;-3;0) và mặt phẳng (P): x + y + z - 3 = 0. Tìm trên (P) điểm M sao cho nhỏ nhất.
Xem lời giải »
Câu 7:
Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
Xem lời giải »
Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và
Mặt cầu có một đường kính là đoạn thẳng vuông góc chung của d1 và d2 có phương trình là:
Xem lời giải »
(tham khảo bài tập 4, trang 105 SGK HH11).
Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0

