Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau d : x= 4-2t ; y = t ; z=3
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau
Phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng trên là:
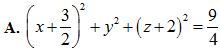
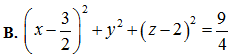
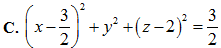
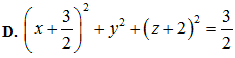
Trả lời:
Chọn B
Đường thẳng d1 có vtcp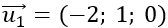 
; đường thẳng d2 có vtcp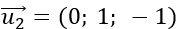 
Giả sử M ∈ d1 => M (4 – 2t; t; 3), N ∈ d2 => N (1; t’; -t’)
Khi đó: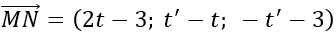 
để MN là đoạn vuông góc chung của d1 và d2 khi:
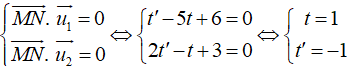
Vậy M (2; 1; 3), N (1; -1; 1)
Mặt cầu cần tìm là mặt cầu đường kính MN nên có tâm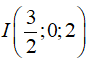 
, bán kính R = MN/2 = 3/2
Và có phương trình là:
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
Xem lời giải »
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (S): x + 2y – 2z + 2018 = 0 và (Q): x + my + (m -1)z + 2017 = 0. Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng (Q)?
Xem lời giải »
Câu 3:
Trong không gian với tọa độ Oxyz, cho hai điểm A (1;1;2), B (-1; 3; -9). Tìm tọa độ điểm M thuộc Oy sao cho vuông tại M.
Xem lời giải »
Câu 4:
Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính bóng bàn. Gọi S1 là tổng diện tích của ba quả bóng bàn, S2 là diện tích xung quanh của hình trụ. Tỉ số S1/S2 bằng:
Xem lời giải »
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n > 0 và m + n = 4. Gọi M là trung điểm của cạnh CC’. Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng:
Xem lời giải »
