Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (x-1)^2 +(y-2)^2
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và mặt phẳng . Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
A.
B.
C.
D.
Trả lời:
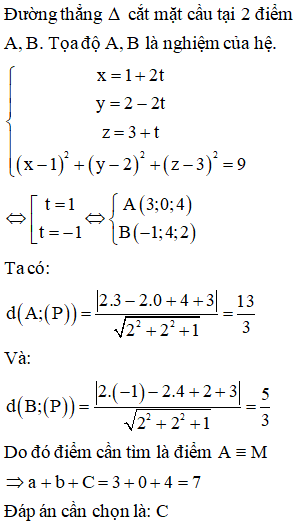
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cắt mặt cầu (S) tâm I(1;-3;3) theo giao tuyến là đường tròn tâm H(2;0;1), bán kính r = 2. Phương trình (S) là:
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho I(2;1;1) và mặt phẳng . Mặt cầu (S) có tâm I cắt (P) theo một đường tròn có bán kính r = 4. Phương trình của mặt cầu (S) là:
Xem lời giải »
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3). Gọi (S) là mặt cầu chứa A, có tâm I thuộc tia Ox và bán kính 7. Phương trình mặt cầu (S) là:
Xem lời giải »
Câu 4:
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt cầu tâm và tiếp xúc với mặt phẳng (Oxz)?
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho mặt cầu và mặt phẳng . Tìm tất cả m để (P) cắt (S) theo giao tuyến là một đường tròn có bán kính lớn nhất.
Xem lời giải »
Câu 6:
Cho điểm A(0;8;2) và mặt cầu (S) có phương trình và điểm B(1;1;-9). Viết phương trình mặt phẳng (P) qua A tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử là vec tơ pháp tuyến của (P). Lúc đó:
Xem lời giải »
Câu 7:
Một vec tơ chỉ phương của đường thẳng là:
Xem lời giải »
Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho ba vec tơ . Tọa độ vec tơ là:
Xem lời giải »

