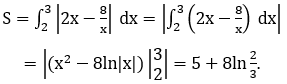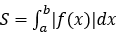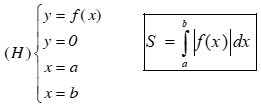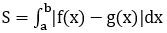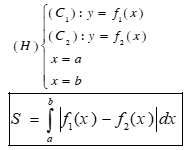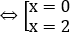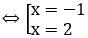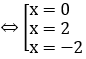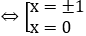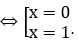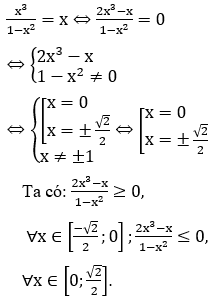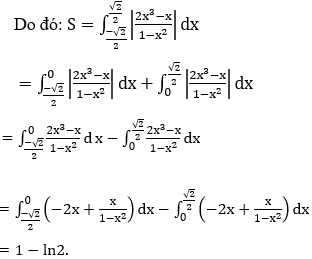Ứng dụng của tích phân Tính diện tích hình phẳng cực hay - Toán lớp 12

---

Ứng dụng của tích phân Tính diện tích hình phẳng cực hay

Với Ứng dụng của tích phân Tính diện tích hình phẳng cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Ứng dụng của tích phân Tính diện tích hình phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

1. Định lý: Cho hàm số y=f(x) liên tục, không âm trên [a;b]. Khi đó diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b là:

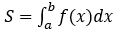
2. Bài toán liên quan

    Bài toán 1: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x=a, x=b được xác định:

    Bài toán 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), y=g(x) liên tục trên đoạn [a;b] và hai đường thẳng x=a, x=b được xác định:

    Chú ý:

- Nếu trên đoạn [a;b], hàm số f(x) không đổi dấu thì:

- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối

    Bài toán 3: Diện tích của hình phẳng giới hạn bởi các đường x=g(y), x=h(y) và hai đường thẳng y=c, y=d được xác định:

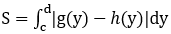
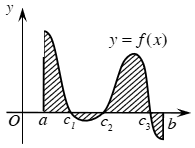
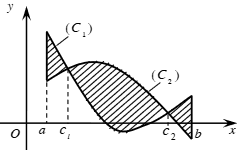
    Bài toán 4: Diện tích hình phẳng giới hạn bởi 2 đồ thị (C₁): f₁(x), (C₂):f₂(x) là:

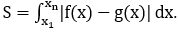
Trong đó: x₁, x_n tương ứng là nghiệm nhỏ nhất của phương trình f(x)=g(x)

Ví dụ minh họa

Bài 1: Tính diện tích S của hình phẳng giới hạn bởi Parabol (P):y=3-x², đường thẳng y=-2x+3, trục tung và x=1.

Hướng dẫn:

Phương trình hoành độ giao điểm: 3-x²=-2x+3 ⇔ x²-2x=0

Diện tích cần tìm được tính bằng công thức sau đây:

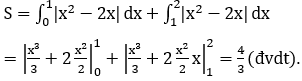
Bài 2: Tính diện tích S của hình phẳng giới hạn bởi các đường y=-2x² và y=-2x-4.

Hướng dẫn:

Phương trình hoành độ giao điểm của y=-2x² và y=-2x-4 là:

-2x²=-2x-4 ⇔ -2x²+2x+4=0

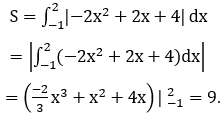
Bài 3: Tính diện tích S của hình phẳng giới hạn bởi các đường y=x³-3x và y=x

Hướng dẫn:

Ta có phương trình hoành độ giao điểm x³-4x=0

Diện tích

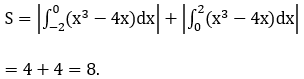
B. Bài tập vận dụng

Bài 1: Tính diện tích hình phẳng được giới hạn bởi các đường y=2x-x² và đường thẳng x+y=2

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số y=x²+x-1 và y=x⁴+x-1 là

x²+x-1=x⁴+x-1 ⇔ x² (x²-1)=0

Ta có: x² (x²-1) ≤ 0 ∀x ∈ [-1;1]. Do đó:

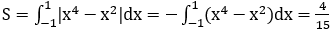
Bài 2: Tính diện tích S của hình phẳng giới hạn bởi các đường x³-x và y=x-x².

Lời giải:

Phương trình hoành độ giao điểm

x³-x=-x²+x ⇔ x=0; x=-2; x=1

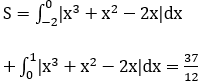
Bài 3: Tính diện tích hình phẳng giới hạn bởi các đường y=cosx; Ox; Oy; x=π

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số y=cosx và trục Ox (y=0) là:

cosx=0 ⇔ x=π/2+kπ(k ∈ Z)

Xét trên [0;π] nên x=π/2.

Do đó

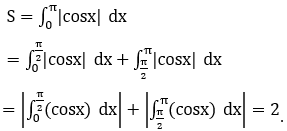
Bài 4: Tính Diện tích hình phẳng giới hạn bởi các đường y=e^x; y=1 và x=1

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=e^x và trục y=1 là:

e^x=1 ⇔ x=0.

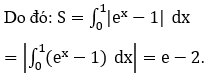
Bài 5: Tính diện tích hình phẳng được giới hạn bởi các đường y=(e+1)x ,y=(1+e^x )x

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=(e+1)x và y=(1+e^x)x là:

(e+1)x = (1+e^x )x

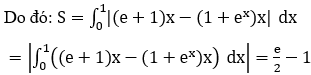
Bài 6: Tính diện tích hình phẳng được giới hạn bởi các đường y=sin2x,y=cosx và hai đường thẳng x=0 ,x=π/2

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=sin2x và y=cosx là:

sin2x=cosx ⇔ cosx.(2sinx-1)=0

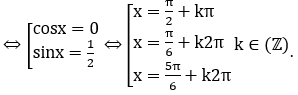
Xét trên [0;π/2] nên nhận x=π/6

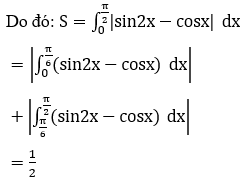
Bài 7: Tính diện tích hình phẳng được giới hạn bởi hai đường y=√x và y=x²

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm sốy=√xvà y=x² là :

x²=√x ⇔ x=x⁴ ⇔ x⁴-x=0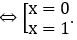

Ta có: x²-√x ≤ 0,∀x ∈ [0;1]. Do đó:

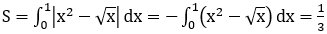
Bài 8: Tính diện tích hình phẳng giới hạn bởi y=sinx; y=cosx; x=0; x=π

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=sinx; y=cosx; x=0; x=π là:

sinx=cosx ⇔ tanx=1 ⇔ x=π/4+kπ,k ∈ Z

Vì x ∈ [0;π] nên x=π/4.

Ta có: sinx-cosx ≤ 0, ∀x ∈ [0;π/4]; sinx-cosx ≥ 0,∀x ∈ [π/4;π]

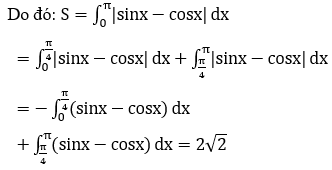
Bài 9: Tính diện tích hình phẳng giới hạn bởi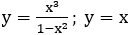

Lời giải:

Bài 10: Tính diện tích hình phẳng giới hạn bởi các đường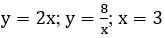

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số y=2x và đồ thị hàm số y=8/x là

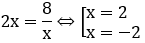
Diện tích hình phẳng cần tìm là: