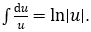Cách tính tích phân hàm số hữu tỉ cực hay - Toán lớp 12

---

Cách tính tích phân hàm số hữu tỉ cực hay

Với Cách tính tích phân hàm số hữu tỉ cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính tích phân hàm số hữu tỉ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Bài toán: Tính 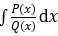. Trong đó P(x) và Q(x) là các đa thức theo biến x có bậc lần lượt là m và n.

    • Trường hợp 1: m ≥ n.

Lấy P(x) chia cho Q(x) để đưa về các nguyên hàm cơ bản.

    • Trường hợp 2: m < n. Phương pháp hệ số bất định

        Bước 1: Đưa Q(x) về dạng Q(x)=(ax+b) (cx+d)ⁿ(px²+qx+r)

(Trong đó px²+qx+r=0 vô nghiệm).

        Bước 2: Đặt

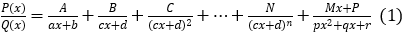
        Bước 3: Quy đồng mẫu và đồng nhất hệ số của (1) để tìm các giá trị A, B, C, …, M, N, P.

Một số trường hợp đặc biệt:

    a) Bậc của P(x) nhỏ hơn bậc của Q(x) 1 đơn vị (m=n-1).

Thử đặt t = Q(x) và tính dt.

    • Nếu dt = k. P(x)dx thì sử dụng

    • Nếu dt ≠ k. P(x)dx thì sử dụng phương pháp hệ số bất định.

    b) Tích phân dạng :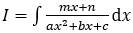

    • Nếu ax²+bx+c=0 có 2 nghiệm phân biệt thì sử ta sử dụng phương pháp hệ số bất định.

    • Nếu ax²+bx+c=0 có nghiệm kép x=x₀ thì 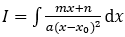, sau đó đặt t=x-x₀.

    • Nếu ax²+bx+c=0 vô nghiệm thì ta sử dụng phương pháp lượng giác hoá.

    c) Một số nguyên hàm cần nhớ:

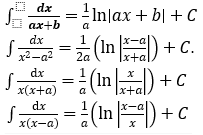
Ví dụ minh họa

Bài 1: Tính tích phân

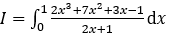
Hướng dẫn:

Bài 2: Tính tích phân

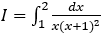
Hướng dẫn:

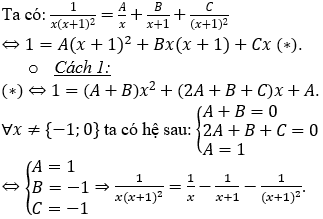
Bài 3: Tính tích phân

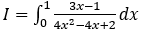
Hướng dẫn:

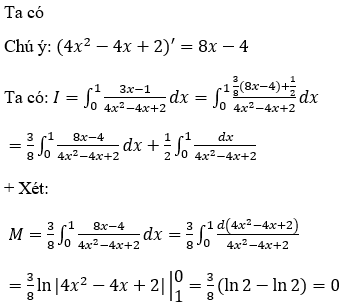
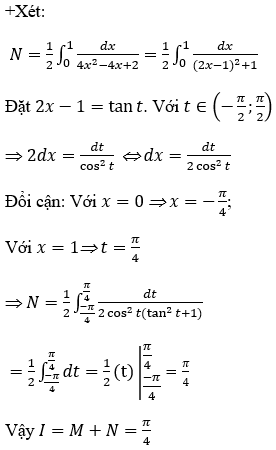
B. Bài tập vận dụng

Bài 1: Tính tích phân

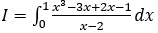
Lời giải:

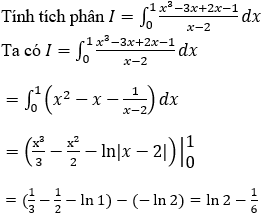
Bài 2: Tính tích phân

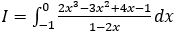
Lời giải:

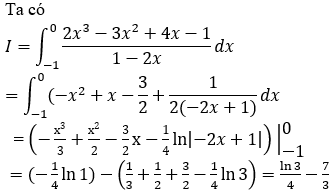
Bài 3: Tính tích phân

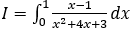
Lời giải:

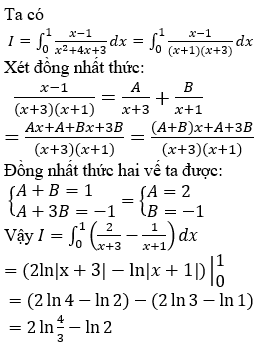
Bài 4: Tính tích phân

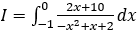
Lời giải:

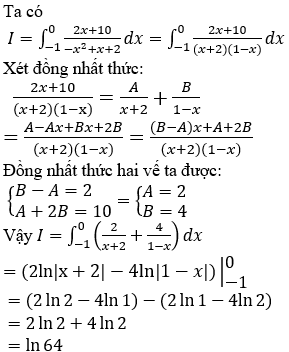
Bài 5: Tính tích phân

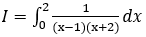
Lời giải:

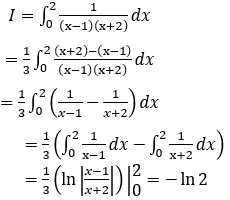
Bài 6: Tính tích phân

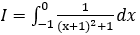
Lời giải:

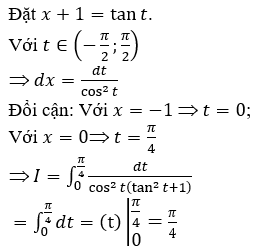
Bài 7: Tính tích phân

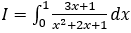
Lời giải:

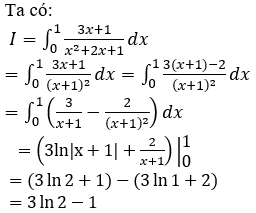
Bài 8: Tính tích phân

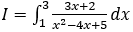
Lời giải:

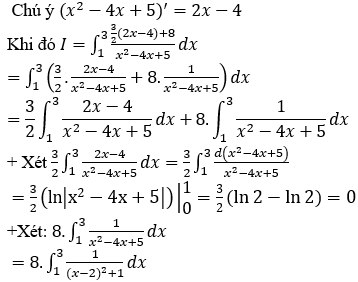
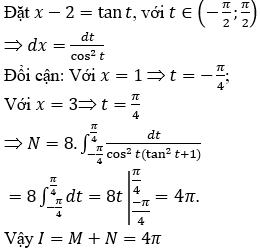
Bài 9: Tính tích phân

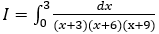
Lời giải:

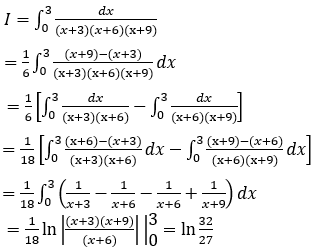
Bài 10: Tính tích phân

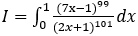
Lời giải: