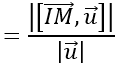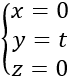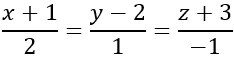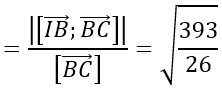Viết phương trình mặt cầu có tâm tiếp xúc đường thẳng cực hay - Toán lớp 12

Viết phương trình mặt cầu có tâm tiếp xúc đường thẳng cực hay

Với Viết phương trình mặt cầu có tâm tiếp xúc đường thẳng cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình mặt cầu có tâm tiếp xúc đường thẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng bài: Viết phương trình mặt cầu biết tâm I (a; b; c) và tiếp xúc với đường thẳng

Phương pháp giải

Do mặt cầu (S) tiếp xúc với mặt phẳng (d) nên khoảng cách từ tâm I đến mặt phẳng (d) bằng bán kính R

Gọi M là điểm bất kì trên d, u→ là vecto chỉ phương của d. Khi đó, khoảng cách từ I đến d được tính theo công thức:

R=d(I;(d))

Khi đó, phương trình mặt cầu cần tìm là:

(S): (x-a)²+(y-b)²+(z-c)²=R²

Ví dụ minh họa

Bài 1: Viết phương trình mặt cầu tâm I (1; -2; 3) và tiếp xúc với trục Oy

Hướng dẫn:

Phương trình đường thẳng Oy là

Vecto chỉ phương của Oy là u→ =(0;1;0)

M (0; 1; 0) ∈ Oy ⇒ IM→=(-1;3; -3)

⇒ [IM→ , u→ ]=(-3;0;1)

Khoảng cách từ I đến trục Oy là:

d(I;(Oy))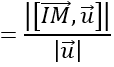= √10

Do mặt cầu tiếp xúc với trục Oy nên khoảng cách từ tâm I đến trục Oy là bán kính của mặt cầu.

Vậy phương trình mặt cầu cần tìm là:

(x-1)²+(y+2)²+(z-3)²=10

Bài 2: Cho điểm A ( -3; 1; 4) và đường thẳng d có phương trình:

Phương trình mặt cầu tâm A, tiếp xúc với d là:

Hướng dẫn:

Đường thẳng d có VTCP u→ =(2; 1; -1) và đi qua điểm M (-1; 2; -3)

Ta có: AM→=(2;1; -7)

[ AM→ , u→ ]=(6; -12;0)

Khoảng cách từ A đến đường thẳng d là:

d(I;(d))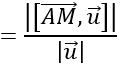= √30

Do mặt cầu tiếp xúc với đường thẳng d nên khoảng cách từ tâm I đến trục d là bán kính của mặt cầu.

Vậy phương trình mặt cầu cần tìm là:

(x+3)²+(y-1)²+(z-4)²=30

Bài 3: Cho điểm I (0; 1; 2); B (-1; 1; 0) và C (2; -3; 1). Viết phương trình mặt cầu có tâm I và tiếp xúc với đường thẳng BC

Hướng dẫn:

Đường thẳng BC có VTCP BC→=(3;-4; 1)

IB→=(-1;0; -4)

[IB→ ; BC→ ]=(16;11; -4)

Khoảng cách từ I đến đường thẳng BC là:

d(I;BC)

Do mặt cầu tiếp xúc với đường thẳng BC nên khoảng cách từ I đến đường thẳng BC là bán kính mặt cầu tâm I

Vậy phương trình mặt cầu cần tìm là:

x²+(y-1)²+(z-2)²=393/26