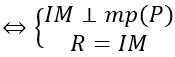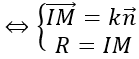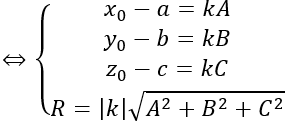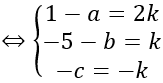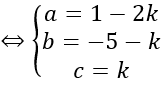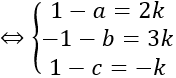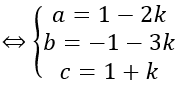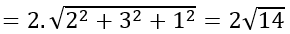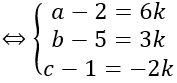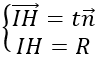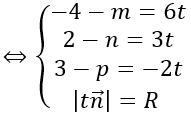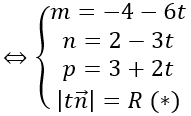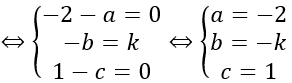Viết phương trình mặt cầu tiếp xúc với mặt phẳng P - Toán lớp 12

Viết phương trình mặt cầu tiếp xúc với mặt phẳng P

Với Viết phương trình mặt cầu tiếp xúc với mặt phẳng P Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình mặt cầu tiếp xúc với mặt phẳng P từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng bài: Viết phương trình mặt cầu tiếp xúc với mặt phẳng (P): Ax + By + Cz + D = 0 tại điểm M (x₀; y₀; z₀) thuộc (P) cho trước

Phương pháp giải

Gọi I (a; b; c) ⇒ IM→=(x₀ - a ; y₀ - b ; z₀ - c)

Mặt phẳng (P) có vecto pháp tuyến n→=(A;B;C)

Mặt cầu tiếp xúc với mặt phẳng (P) tại điểm M

Sử dụng các điều kiện cho trước để tìm k

⇒ I; R

Ví dụ minh họa

Bài 1: Cho hai mặt phẳng (P) và (Q) có phương trình (P): x – 2y + z – 1 = 0 và (Q): 2x + y – z + 3 = 0. Viết phương trình mặt cầu có tâm nằm trên mặt phẳng (P) và tiếp xúc với mặt phẳng (Q) tại điểm M, biết rằng M thuộc mặt phẳng (Oxy) và có hoành độ x_M=1

Hướng dẫn:

Điểm M thuộc mặt phẳng Oxy và có hoành độ x_M=1 nên M (1; y₀; 0)

Mặt khác M thuộc mặt phẳng Q nên 2. 1 + y₀ + 3 = 0 ⇒ y₀ =-5

⇒ M (1; -5;0)

Gọi I (a; b; c) là tâm mặt cầu

⇒ IM→=(1-a; -5-b; -c)

Mặt phẳng (Q) có vecto pháp tuyến n→=(2;1;-1)

Do mặt cầu tiếp xúc với (Q) tại điểm M nên IM→ vuông góc với mặt phẳng (Q)

⇒ IM→= k n→

Mặt khác I thuộc mặt phẳng (P) nên tọa độ của I thỏa mãn phương trình mặt phẳng (P)

⇒ a-2b+c-1=0

⇔ 1-2k+2(5+k)+k-1=0

⇔ k=-10

Với k=-10 thì I (21; 5; -10)

Bán kính của mặt cầu là R=|IM→ |=|k n→ |

= 10√6

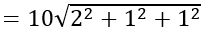
Vậy phương trình mặt cầu cần tìm là:

(x-21)² +(y-5)² +(z+10)² =600

Bài 2: Cho hai mặt phẳng (P): 2x + 3y - z + 2 = 0, (Q): 2x - y - z + 2 = 0. Viết phương trình mặt cầu (S) tiếp xúc với mặt phẳng (P) tại điểm A (1; -1; 1) và có tâm thuộc mặt phẳng (Q)

Hướng dẫn:

Gọi I (a; b; c) là tâm của mặt cầu

⇒ IA→=(1-a; -1-b; 1-c)

Mặt phẳng (P) có vecto pháp tuyến n→=(2;3;-1)

Do mặt cầu tiếp xúc với (P) tại điểm A nên IA→ vuông góc với mặt phẳng (P)

⇒ IA→= k n→

Lại có I thuộc mặt phẳng (Q) nên ta có:

2a-b-c+2=0

⇔ 2(1-2k)+(1+3k)-1-k+2=0

⇔ k=2

Với k = 2 thì I (-3; -7; 3)

Bán kính mặt cầu: R=|IA→ |=|k n→ |

Vậy phương trình mặt cầu cần tìm là:

(x+3)² +(y+7)² +(z-3)²=56

Bài 3: Cho điểm A(2; 5; 1) và mặt phẳng (P): 6x + 3y - 2z + 24 = 0, H là hình chiếu vuông góc của A trên mặt phẳng (P). Viết phương trình mặt cầu (S) có diện tích 784π và tiếp xúc với mặt phẳng (P) tại H, sao cho điểm A nằm trong mặt cầu.

Hướng dẫn:

Gọi H (a; b; c).

⇒ AH→=(a-2;b-5;c-1)

Mặt phẳng (P) có vecto pháp tuyến n→=(6;3;-2)

Do H là hình chiếu vuông góc của A trên mặt phẳng (P) nên AH→ vuông góc với mặt phẳng (P).

⇒ AH→ =k n→

Lại có H thuộc (P) nên 6a + 3b – 2c + 24 = 0

⇔ 6(6k+2)+3(3k+5)-2(-2k+1)+24=0

⇔ k=-1

⇒ H(-4;2;3)

Gọi R là bán kính mặt cầu.

Mặt cầu (S) có diện tích là 784π

⇒ 4πR² =784π ⇒ R=14

Gọi I (m, n, p) là tâm mặt cầu

⇒ IH→=(-4-m;2-n;3-p)

Do mặt cầu tiếp xúc với mặt phẳng (P) tại H nên ta có

Xét (*): |t n→ |=R

=14 ⇔ |t|=2 ⇔ t= ±2

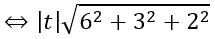
Với t = 2 ta có I (-16; -4; 7)

Khi đó:

IA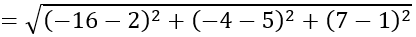=21>R

⇒ A nằm ngoài mặt cầu.

Với t = - 2 ta có I (8; 8; -1)

Khi đó

IA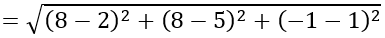= 7<R

⇒ A nằm trong mặt cầu.

Vậy phương trình mặt cầu cần tìm là:

(x-8)² +(y-8)² +(z+1)²=196

Bài 4: Viết phương trình của mặt cầu (S) biết (S) tiếp xúc với mặt phẳng tọa độ Oxz tại điểm M(- 2;0;1) và (S) đi qua điểm A(2;2;1)

Hướng dẫn:

Gọi I (a; b; c) là tọa độ tâm của mặt cầu.

⇒ IM→=(-2-a; -b;1-c)

Mặt phẳng (Oxz) có vecto pháp tuyến n→=(0 ;1 ;0)

Do mặt cầu (S) tiếp xúc với mặt phẳng tọa độ (Oxz) tại M nên

Giải (1) :

IM→= k n→

Do mặt cầu đi qua A(2; 2;1) nên IA = R

Ta có : IA² =4² +(k+2)² =k² +4k +20

Từ (2) ⇒ IA² =R² =k² ⇒ k² +4k +20 =k²

⇒ k=-5

Vậy I (-2 ; 5 ; 1) và R = 5

Phương trình mặt cầu cần tìm là :

(x+2)² +(y-5)² +(z-1)²=25