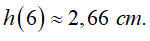Ứng dụng của tích phân tính diện tích, thể tích, quãng đường, vận tốc cực hay - Toán lớp 12

---

Ứng dụng của tích phân tính diện tích, thể tích, quãng đường, vận tốc cực hay

Với Ứng dụng của tích phân tính diện tích, thể tích, quãng đường, vận tốc cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Ứng dụng của tích phân tính diện tích, thể tích, quãng đường, vận tốc từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1. Diện tích hình phẳng

Dạng 1.1. Tính diện tích hình phẳng

1. Phương pháp giải

* Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a;b] , trục hoành và hai đường thẳng x=a; x= b được xác định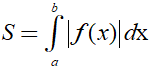

* Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a;b] và hai đường thẳng x=a; x= b được xác định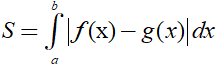

- Nếu trên đoạn [a; b], hàm số f(x) không đổi dấu thì: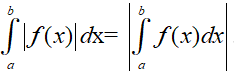

- Diện tích của hình phẳng giới hạn bởi các đường x= g(y),x=h(y) và hai đường thẳng y = c; y= d được xác định: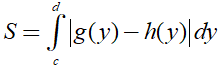

2. Ví dụ minh họa

Ví dụ 1. Diện tích hình phẳng được giới hạn bởi các đường y= x² + x − 1 và y = x⁴ + x − 1 là:

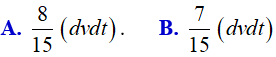
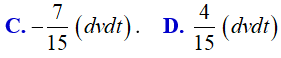
Lời giải:

Đáp án: D

Phương trình hoành độ giao điểm của đồ thị hàm số y = x² + x − 1 và y = x⁴ + x − 1 là :

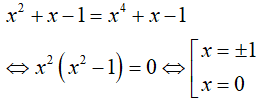
Ta có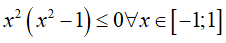

Do đó

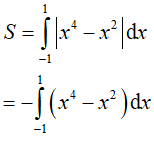
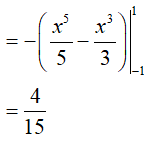
Ví dụ 2. Tính diện tích hình phẳng giới hạn bởi y = x² − 4|x| + 3 và trục hoành?

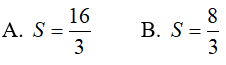
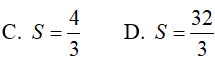
Lời giải:

Đáp án: A

Phương trình hoành độ giao điểm

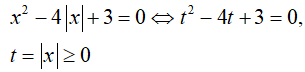
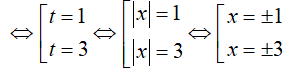
Do hàm số y= x² − 4 |x| + 3 là hàm chẵn nên diện tích hình phẳng cần tính là:

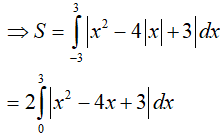
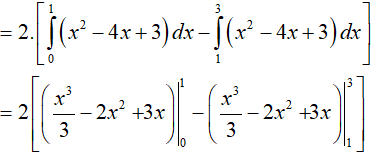
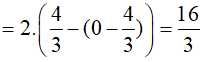
Vậy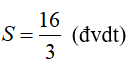

Ví dụ 3. Tính diện tích hình phẳng giới hạn bởi y = |x² − 1|, y = |x| + 5

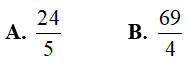
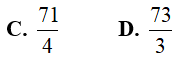
Lời giải:

Đáp án: D

Phương trình hoành độ giao điểm của hai đồ thị:

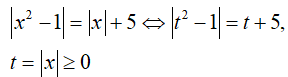
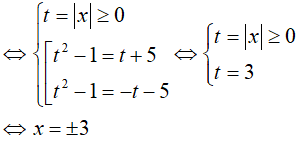
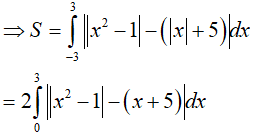
(Do hàm số y= |x|+ 5 là hàm số chẵn)

Bảng xét dấu

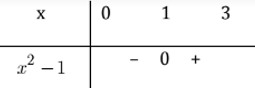
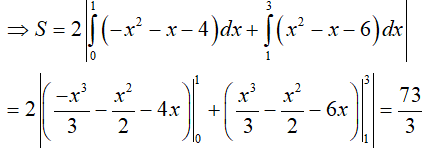
Vậy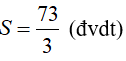

Ví dụ 4. Diện tích của hình phẳng giới hạn bởi: (C): y = √x; d:y = x − 2; Ox là:

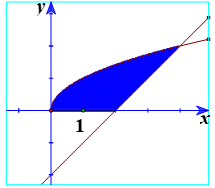
Lời giải:

Đáp án: A

* Phương trình hoành độ giao điểm của đường cong (C) với đường thẳng d là: √x = x − 2 ⇔ x = 4

*Phương trình hoành độ giao điểm của đường cong (C) với trục hoành là: √x = 0 ⇔ x = 0

* Phương trình hoành độ giao điểm của đường thẳng d với trục hoành là: x − 2 = 0 ⇔ x= 2

Diện tích hình phẳng cần tìm là:

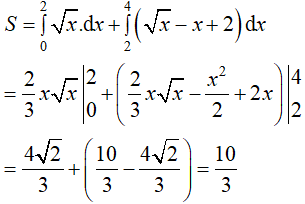
Ví dụ 5. Diện tích hình phẳng giới hạn bởi y = sinx, y = cosx, x = 0; x = π là:

A.2.    B.3.    C.3√2.    D. 2√2.

Lời giải:

Đáp án: D

Phương trình hoành độ giao điểm của hai đồ thị hàm số y= sinx, y= cosx là:

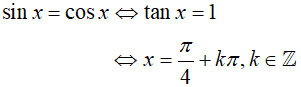
Vì x ∈ [0; π] nên .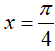

Ta có:

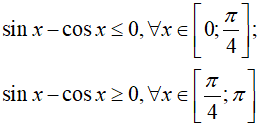
Do đó:

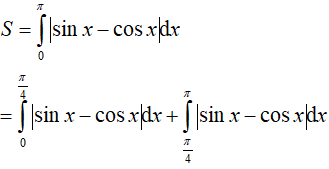
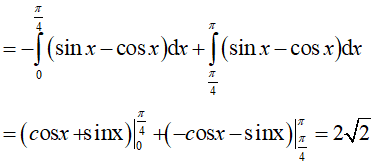
Dạng 1.2. Tìm tham số m để diện tích hình phẳng bằng S₀

1. Phương pháp giải

+ Bước 1. Tính diện tích hình phẳng (H).

+ Bước 2. Lập phương trình ẩn m, giải m.

2. Ví dụ minh họa

Ví dụ 1. Diện tích hình phẳng giới hạn bởi đồ thị y= m.x.cosx, trục Ox, x= 0 và x = π bằng 3π. Khi đó giá trị của m là:

A. m= − 3    B. m= 3    C. m = −4    D. ±3.

Lời giải:

Đáp án: D

Ta có diện tích hình phẳng cần tính là:

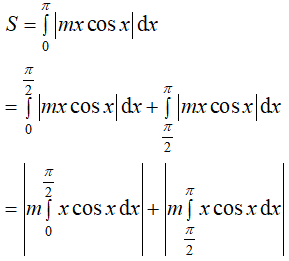
Đặt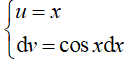

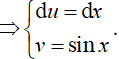
Khi đó

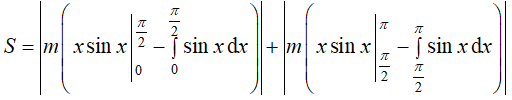
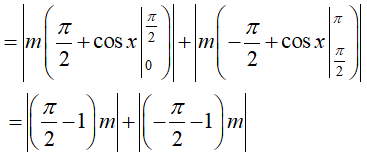
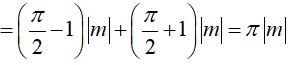
Theo giả thiết S = 3π ⇔ r|m| = 3π ⇔ m = ±3 .

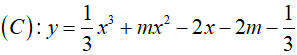
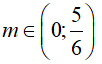
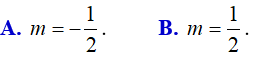
Ví dụ 2. Cho . Giá trị sao cho hình phẳng giới hạn bởi đồ thị (C), y= 0; x= 0; x= 2 có diện tích bằng 4 là

Lời giải:

Đáp án: B

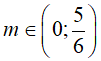
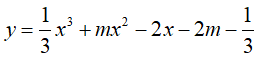
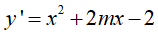
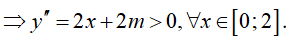
Với mọi , xét hàm số có ,

Mặt khác,

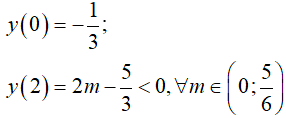
Do đó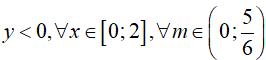

Diện tích hình phẳng là:

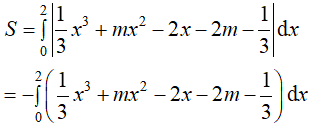
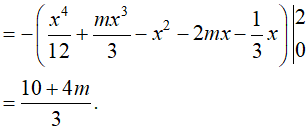
Theo giả thiết

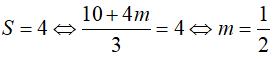
Vậy

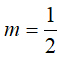
Ví dụ 3. Diện tích hình phẳng giới hạn bởi hai đường cong y² = ax, x² = ay ( a > 0) là 3. Tìm a.

A. 1    B. 2    C. 3    D. 6

Lời giải:

Đáp án: C

Hệ phương trình tọa độ giao điểm của 2 đường cong trên là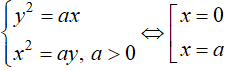

Khi đó hình phẳng cần tìm được tạo bởi đồ thị các hàm số: 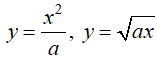và các đường thẳng x= 0; x= a (a > 0).

Diện tích hình phẳng cần tìm là:

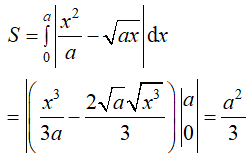
Theo giả thiết, diện tích hình phẳng giới hạn bởi hai đường cong đã cho là 3 nên ta có: 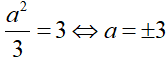. Mà a > 0 nên a= 3.

Dạng 2. Thể tích vật thể và thể tích khối tròn xoay

1. Phương pháp giải

a. Thể tích vật thể

Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm a a ≤ x ≤ b. Giả sử S(x) là hàm số liên tục trên đoạn [a; b]. Thể tích của B là:

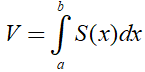
b. Thể tích khối tròn xoay

Cho hàm số y= f(x) liên tục; không âm trên [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y=f(x); trục hoành và hai đường thẳng x=a; x=b quay quanh trục Ox tạo nên một khối tròn xoay. Thể tích của nó là:

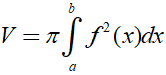
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x= g(y), trục tung và hai đường thẳng y=c; y= d quay quanh trục Oy là:

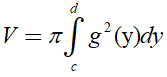
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y= f(x); y= g(x) và hai đường thẳng x=a; x= b quay quanh trục Ox:

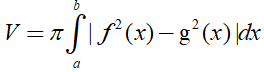
2. Ví dụ minh họa

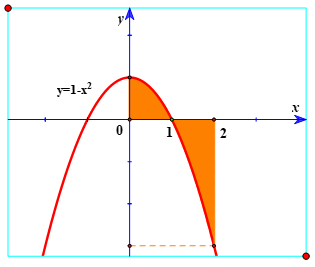
Ví dụ 1. Thể tích khối tròn xoay được giới hạn bởi các đường y = (1 − x²); y = 0; x = 0 và x= 2 khi quay quanh trục Ox bằng:

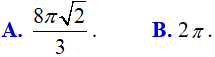
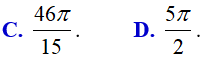
Lời giải:

Đáp án: C

Thể tích khối tròn xoay được giới hạn bởi các đường y= (1 − x²); y = 0 ; x= 0 và x=2 khi quay quanh trục Ox là:

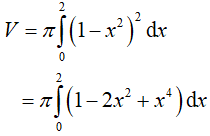
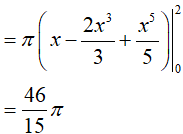
Ví dụ 2. Cho hình phẳng (H) được giới hạn bởi đường cong 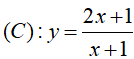, trục Ox và trục Oy. Thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox là:

A. 3π.    B. 4πln2.    C. (3 − 4ln2)π.    D. (4 − 3ln2)π.

Lời giải:

Đáp án: C

Phương trình hoành độ giao điểm: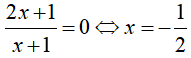

Suy ra:

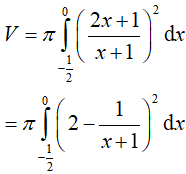
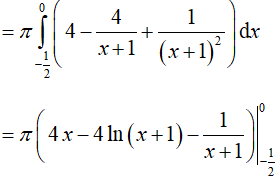
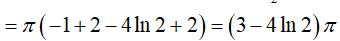
Ví dụ 3. Tính thể tích hình khối do hình phẳng giới hạn bởi các đường x = −y² + 5; x = 3 − y quay quanh Oy

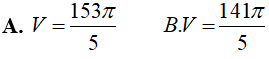
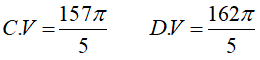
Lời giải:

Đáp án: A

Tung độ giao điểm −y² + 5 = 3 − y ⇔ −y² + y + 2 = 0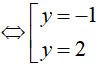

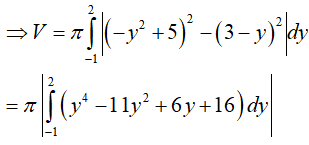
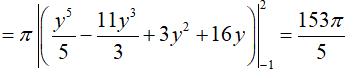
Vậy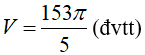

Ví dụ 4. Thể tích khối tròn xoay giới hạn bởi y= lnx, y=0, x= e quay quanh trục Ox có kết quả là:

A. πe.    B. π(e − 1).    C. π(e − 2).    D. π(e + 1).

Lời giải:

Đáp án: C

Xét phương trình: lnx = 0, x > 0 ⇔ x= 1 .

Thể tích khối tròn xoay cần tính là:

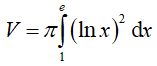
Đặt u = ln²x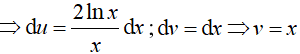

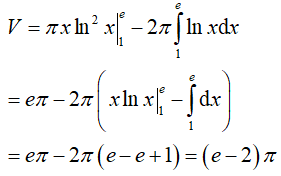
Dạng 3. Ứng dụng của tích phân để tính quãng đường, vận tốc của chuyển động.

1. Phương pháp giải

* Cho vật chuyển động có phương trình vận tốc v= v(t). Quãng đường vật đi được từ t₀ đến t₁ là :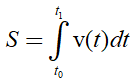

2. Ví dụ minh họa

Ví dụ 1. Một vật chuyển động chậm dần đều với vận tốc v(t)= 160 − 10t (m/s). Quãng đường mà vật chuyển động từ thời điểm t = 0 (s) đến thời điểm mà vật dừng lại là

A.1028 m    B. 1280 m    C. 1380 m    D.1308 m

Lời giải:

Đáp án: B

Khi vật dừng lại thì v(t) = 160 − 10t ⇔ t = 16

Suy ra:

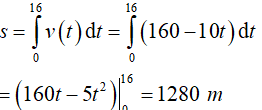
Ví dụ 2. Một chiếc ô tô chuyển động với vận tốc v(m/s), có gia tốc 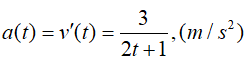. Vận tốc của ô tô sau 10 giây (làm tròn đến hàng đơn vị) là

A.4,6 m/s.    B. 7,2 m/s    C. 1,5 m/ s    D. 2,2 m/s

Lời giải:

Đáp án: A

Vận tốc của ô tô sau 10 giây là:

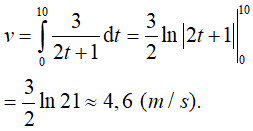
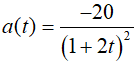
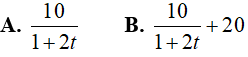
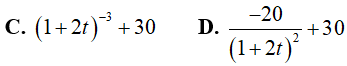
Ví dụ 3. Một hạt proton di chuyển trong điện trường có biểu thức gia tốc ( theo cm²/s) là (với t tính bằng giây).Tìm hàm vận tốc v theo t,biết rằng khi t=0 thì v=30 (cm/s)

Lời giải:

Đáp án: B

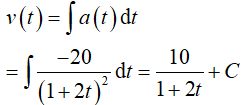
Do v(0) = 30, suy ra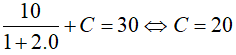

Vậy, hàm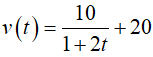

Ví dụ 4. Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a(t)= 3t +t². Tính quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc

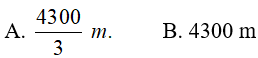
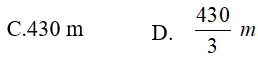
Lời giải:

Đáp án: A

Hàm vận tốc:

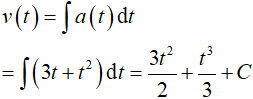
Lấy mốc thời gian lúc tăng tốc => v(0)= 10 => C =10

Ta được: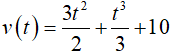

Sau 10 giây, quãng đường vật đi được là:

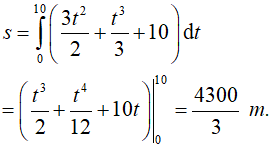
Ví dụ 5. Gọi h(t) (cm) là mức nước trong bồn chứa sau khi bơm được t giây. Biết rằng 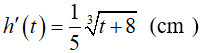và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (chính xác đến 0,01 cm)

A. 2,67 cm    B. 2,66 cm    C. 2,65 cm    D. 2,68cm

Lời giải:

Đáp án: B

Hàm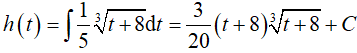

Lúc t = 0, bồn không chứa nước.

Suy ra

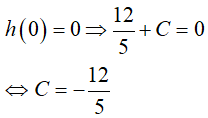
Vậy, hàm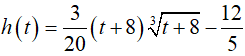

Mức nước trong bồn sau 6 giây là