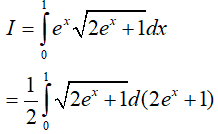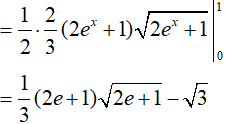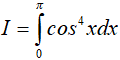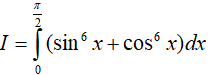Phương pháp tính tích phân cơ bản cực hay - Toán lớp 12
Phương pháp tính tích phân cơ bản cực hay
Với Phương pháp tính tích phân cơ bản cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính tích phân từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
Dạng 1. Tính chất của tích phân
1. Phương pháp giải
Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a,b,c là ba số bất kỳ thuộc K. Khi đó ta có
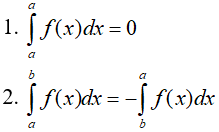
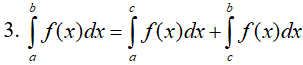
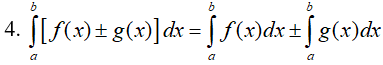
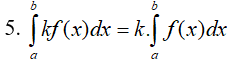
Nếu f(x) ≥ 0, ∀x ∈ [a, b] thì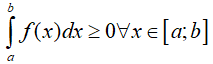 
Nếu ∀x ∈ [a, b]: f(x) ≥ g(x)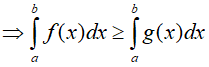 
Nếu ∀x ∈ [a, b] nếu M ≤ f(x) ≤ N thì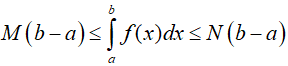 
2. Ví dụ minh họa
Ví dụ 1. Cho tích phân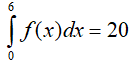 
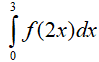
. Tính tích phân 
A . I= 40 B. I= 10 C. I= 20 D. I= 5
Lời giải:
Đáp án: B
Đặt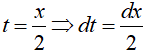 
Đổi cận: với x = 0 => t = 0
Với x = 6 => t = 3
Ta có:
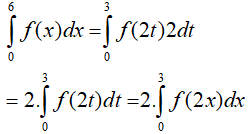
Suy ra: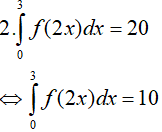 
Ví dụ 2. Cho hàm số y= f(x) liên tục trên đoạn [0; 6] thỏa mãn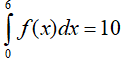 
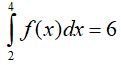
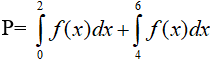
và 
. Tính giá trị của biểu thức 
A. P= 4 B. P= 16 C. P= 8 D. P= 10
Lời giải:
Đáp án: A
Ta có:
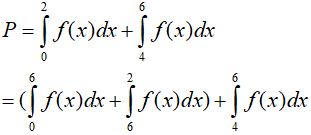
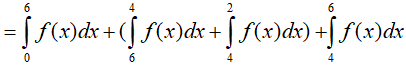
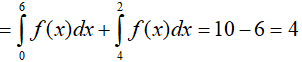
Ví dụ 3. Cho hàm số f(x) liên tục trên R và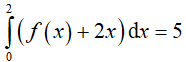 
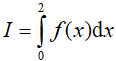
. Tính 
.
A. I= 9 B. I= 1 C. I = − 1 D. I = −9
Lời giải:
Đáp án: B
Ta có:
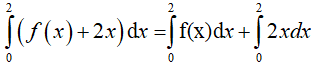
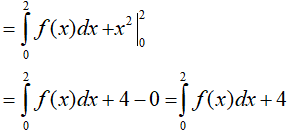
Kết hợp với giả thiết suy ra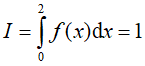 
Ví dụ 4. Cho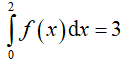 
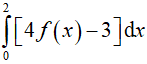
. Khi đó 
bằng
A. 2 B. 4 C. 6 D. 8
Lời giải:
Đáp án: C
Ta có:
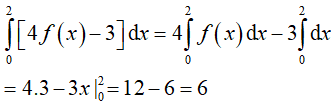
Dạng 2. Tính trực tiếp
1. Phương pháp giải
Cho hàm số y= f(x) liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì: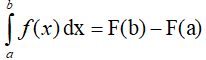 
.
Như vậy, để tính tích phân của 1 hàm số ta cần:
• Bước 1: Xác định F(x) là nguyên hàm của hàm số.
• Bước 2. Tính F(b) − F(a).
Dạng 2.1. Hàm đa thức
2. Ví dụ minh họa
Ví dụ 1. Tích phân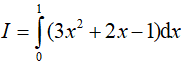 
bằng
A.I=1 B.I= 2 C.I= 3 D. I= −1
Lời giải:
Đáp án: A
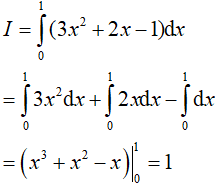
Ví dụ 2. Có bao nhiêu giá trị của m sao cho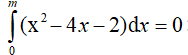 
:
A.1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: A
Ta có:
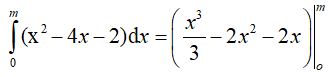
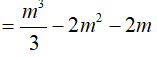
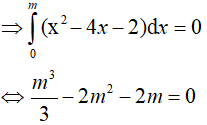
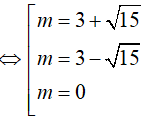
Vậy có 3 giá trị của m thỏa mãn.
Ví dụ 3. Tích phân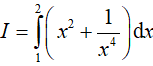 
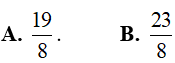
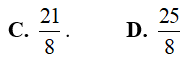
bằng
Lời giải:
Đáp án: C
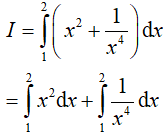
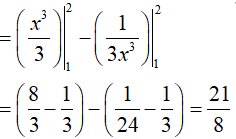
Ví dụ 4. Tính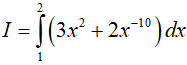 
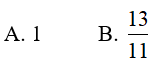
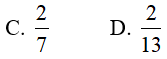
Lời giải:
Đáp án: B
Ta có:
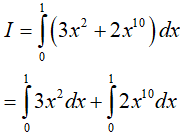
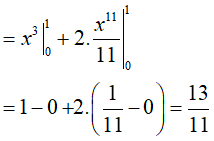
Ví dụ 5. Tích phân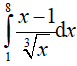 
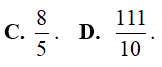
bằng
Lời giải:
Đáp án: A
Do x ∈ (1; 8) => x > 0 nên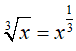 
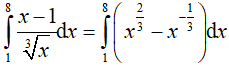
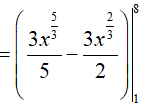
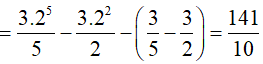
. Vì vậy
Dạng 2.2. Hàm phân thức
Ví dụ minh họa
Ví dụ 1. Tích phân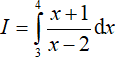 
bằng
Lời giải:
Đáp án: D
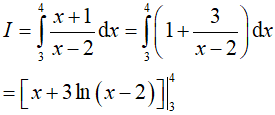
Ví dụ 2. Tích phân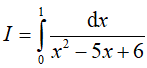 
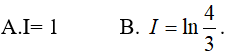
bằng
Lời giải:
Đáp án: B
Ta có:
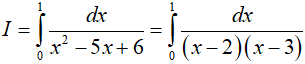
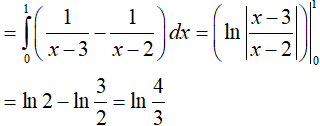
Ví dụ 3. Cho tích phân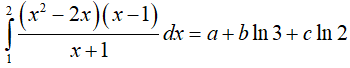 
(a,b,c ∈ Q). Chọn khẳng định đúng trong các khẳng định sau:
A. a < 0 B. c < 0 C. b > 0 D. a + b + c > 0
Lời giải:
Đáp án: D
Ta có:
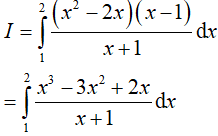
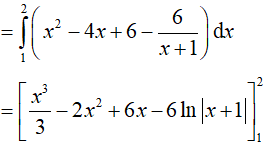
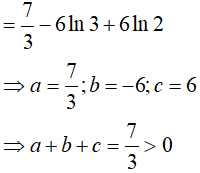
Ví dụ 4. Tính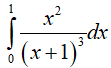 
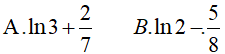
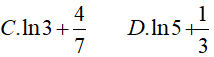
Lời giải:
Đáp án: B
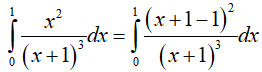
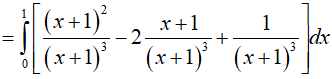
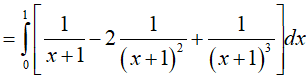
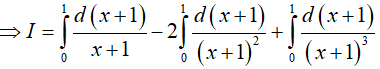
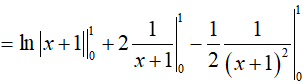
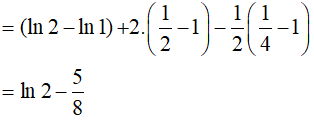
Ví dụ 5. Tính tích phân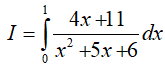 
A . 2ln3 − ln2 B. ln3 − 2ln2 C. 2ln3 − 3ln2 D. 3ln2 +2ln3
Lời giải:
Đáp án: A
Cách 1: (Hệ số bất định)
Ta có:
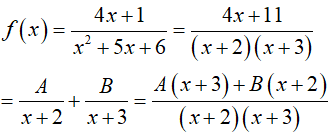
Thay x= −2 vào hai tử số: 3= A và thay x= −3 vào hai tử số: −B= −1 suy ra B= 1
Do đó
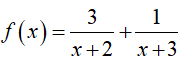
Vậy:
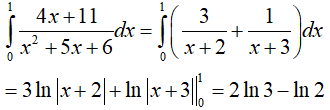
Cách 2
Ta có:
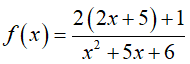
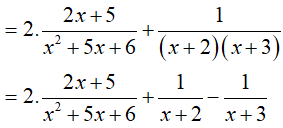
Do đó
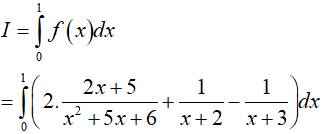
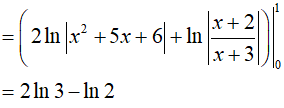
Dạng 2.3. Hàm căn thức
Ví dụ minh họa
Ví dụ 1. Tính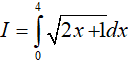 
Lời giải:
Đáp án: C
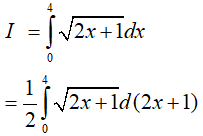
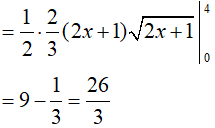
Ví dụ 2. Tính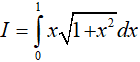 
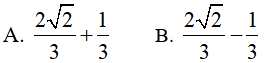
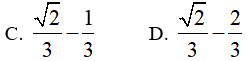
Lời giải:
Đáp án: B
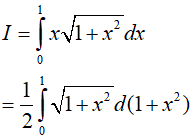
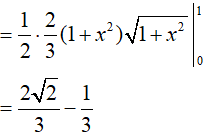
Ví dụ 3. Tính
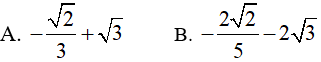
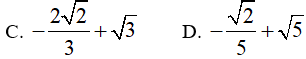
Lời giải:
Đáp án: D
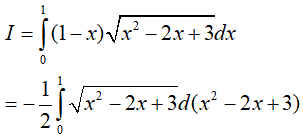
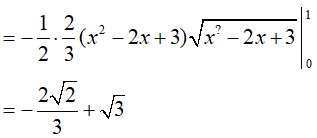
Ví dụ 4. Tính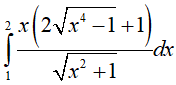 
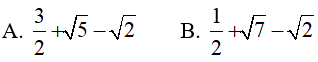
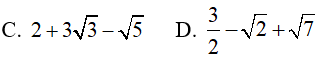
Lời giải:
Đáp án: A
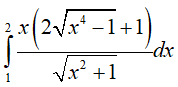
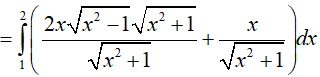
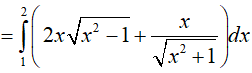
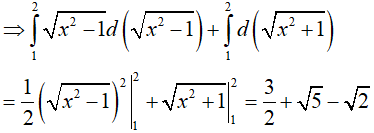
Ví dụ 5. Tính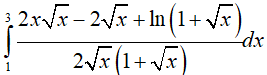 
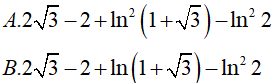
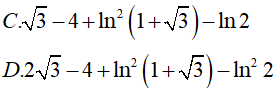
Lời giải:
Đáp án: D
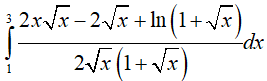
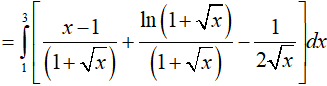
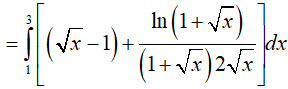
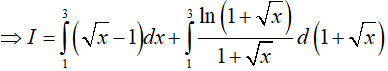
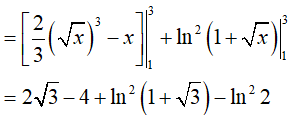
Dạng 2.4. Hàm lượng giác
2. Ví dụ minh họa
Ví dụ 1. Tích phân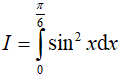 
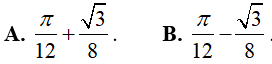
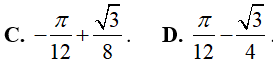
có giá trị là
Lời giải:
Đáp án: B
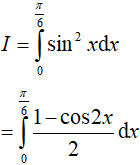
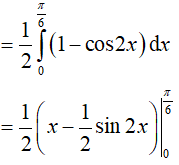
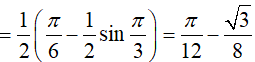
Ví dụ 2. Tích phân 
có giá trị là
Lời giải:
Đáp án: A
Ta có
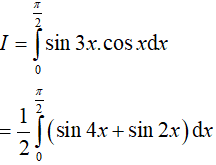
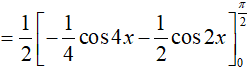
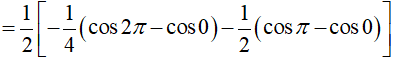
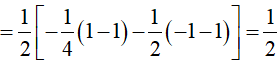
Ví dụ 3. Giả sử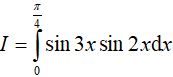 
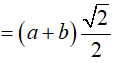
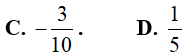
khi đó a+ b là
Lời giải:
Đáp án: B
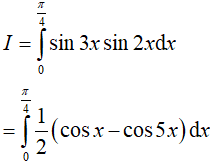
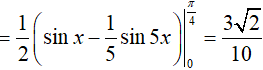
Suy ra
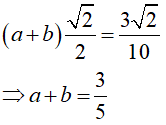
Vậy
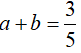
Ví dụ 4. Tính 
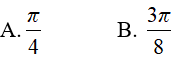
Lời giải:
Đáp án: B
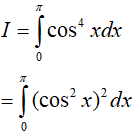
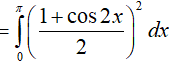
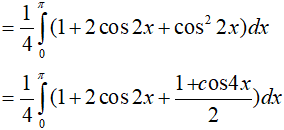
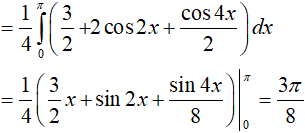
Ví dụ 5. Tính 
Lời giải:
Đáp án: A
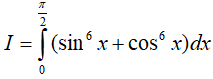
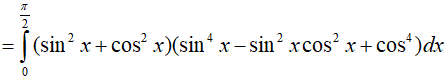
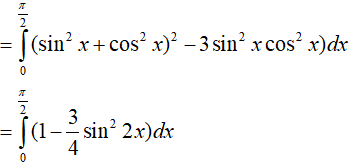
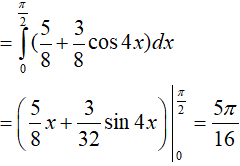
Dạng 2.5. Hàm mũ, logarit
2. Ví dụ minh họa
Ví dụ 1. Tích phân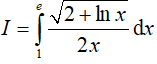 
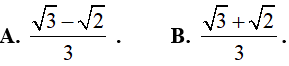
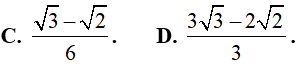
bằng
Lời giải:
Đáp án: D
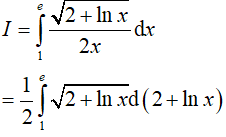
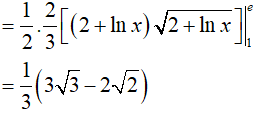
Vậy: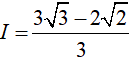 
Ví dụ 2. Tích phân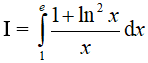 
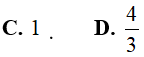
có giá trị là:
Lời giải:
Đáp án: D
Ta có:
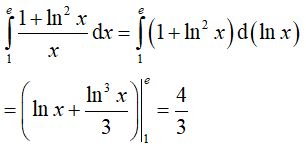
Ví dụ 3. Tính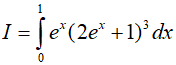 
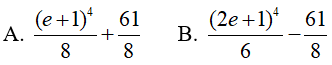
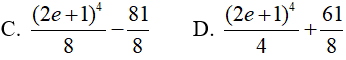
Lời giải:
Đáp án: C
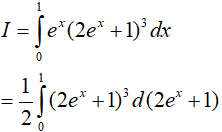
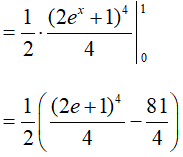
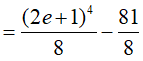
Ví dụ 4. Tính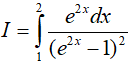 
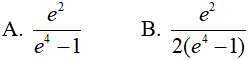
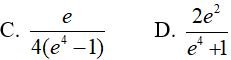
Lời giải:
Đáp án: B
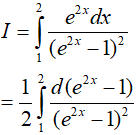
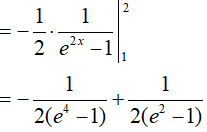
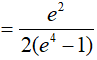
Ví dụ 5. Tính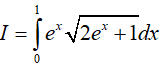 
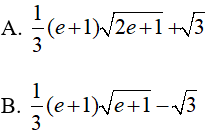
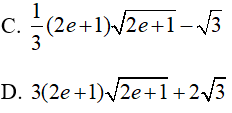
Lời giải:
Đáp án: C
