Bài tập Dạng lượng giác của số phức trong đề thi Đại học có lời giải (4 dạng) - Toán lớp 12
Bài tập Dạng lượng giác của số phức trong đề thi Đại học có lời giải (4 dạng)
Với Bài tập Dạng lượng giác của số phức trong đề thi Đại học có lời giải (4 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập lượng giác của số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1: Viết số phức dưới dạng lượng giác
1. Phương pháp giải
*Định nghĩa: Cho số phức z ≠ 0 . Gọi M là điểm trong mặt phẳng phức biểu diễn số z. Số đo (radian) của mỗi góc lượng giác tia đầu Ox, tia cuối OM được gọi là một acgumen của z.
* Cho số phức z = a+ bi, (a,b ∈ R) Để viết số phức z dưới dạng lượng giác ta làm như sau:
+ Tìm một acgumen của số phức z là φ
+ Tính môđun của số phức z: |z| = r =
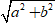
+ Khi đó, ta có z = r.(cosφ + i.sinφ)
2. Ví dụ minh họa
Ví dụ 1: Viết số phức z = 6 + 6i dưới dạng lượng giác?
A. z = 6√2(cos

B. z = 6(cos

C. z = 3√2(cos

D. z = 3√2(cos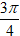
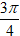
Lời giải:
Ta có: |z| = r = 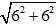
Chọn φ là số thực thoả mãn
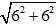
⇒ φ = 
Do đó, dạng lượng giác của số phức z là:
z = 6√2(cos

Chọn A.
Ví dụ 2: Viết số 10 dưới dạng lượng giác?
A. 10.(cosπ + isinπ)
B. 10.(cos 0 + i.sin0)
C. 10√2(cos

D. 10√2(cos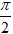
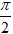
Lời giải:
Ta có: Số 10 có mô dun là 10 và có một acgumen bằng 0 nên nó có dạng lượng giác là:
10.(cos0 + i.sin0).
Chọn B.
Ví dụ 3: Viết số -

A. - 
B. 
C. 
D. - 
Lời giải:
Số - 

- 

Chọn C.
Ví dụ 4: Viết số phức z =
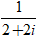
A. 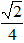
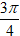
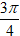
B. 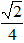


C. 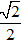
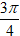
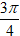
D. 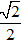


Lời giải:
Ta có: z = 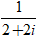
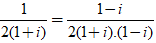
= 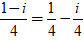
Ta có |z| = 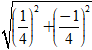
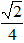
Một acgumen là φ thỏa mãn:
cosφ = 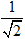
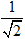

Do đó ,dạng lượng giác của số phức z là:
z = 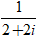
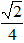


Chọn B.
Ví dụ 5: Viết số phức z = 100i dưới dạng lượng giác?
A. z = 100.√2(cos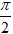
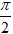
B. z = 100.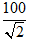
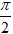
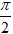
C. z = 100.√2(cos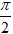
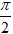
D. z = 100(cos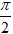
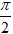
Lời giải:
Ta có: |z| = 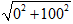
Gọi φ là một acgumen của z thì φ thỏa mãn: cosφ = 0; sinφ = 1 ⇒ φ =
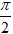
Do đó, dạng lượng giác của số phức z là :
z = 100(cos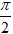
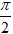
Chọn D.
Dạng 2: Nhân, chia số phức dạng lượng giác
1. Phương pháp giải
Nếu z = r.(cosφ + i.sinφ) và
z' = r'.(cosφ' + i.sinφ'); (r ≥ 0; r' ≤ 0)
Thì
z.z' = r.r'[cos(φ + φ') + i.sin(φ + φ')]
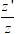
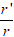
2. Ví dụ minh họa
Ví dụ 1: Viết số phức sau dưới dạng lượng giác z = (1 - i√3).(1 + i)
A. z = 2√2[cos(- 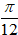
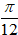
B. z = 2[cos(- 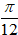
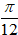
C. z = 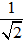
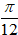
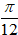
D. Đáp án khác
Lời giải:
Ta có:
1 - i√3 = 2.[cos(- 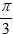
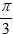
1 + i = √2[cos

Áp dụng công thức nhân, chia số phức ta đuợc:
z = (1 - i√3)(1 + i)
= 2√2[cos(- 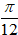
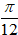
Chọn A.
Ví dụ 2: Viết số phức sau dưới dạng lượng giác z =
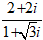
A. 2[cos- 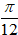
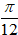
B. 2√2[cos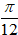
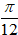
C. √2[cos- 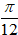
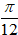
D. 
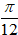
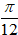
Lời giải:
Ta có: 2 + 2i = 2√2[cos

Và 1 + √3i = 2.[cos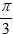
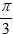
Do đó: z = 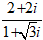
= 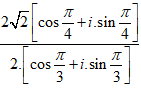
= √2[cos- 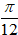
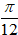
Chọn C.
Ví dụ 3: Viết số phức sau dưới dạng lượng giác z =
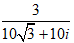
A. 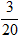


B. 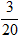


C. 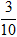


D. 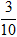


Lời giải:
Ta có: 3 = 3.(cos0 + i.sin0)
10√3 + 10i = 20.(cos

Do đó, z = 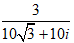
= 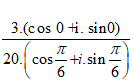
= 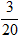


Chọn B.
Ví dụ 4: Viết số phức sau dưới dạng lượng giác z =
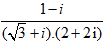
A. 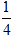
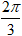
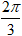
B. 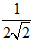
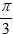
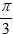
C. 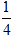
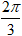
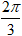
D. Đáp án khác
Lời giải:
Ta có: √3 + i = 2(cos

2 + 2i = 2√2.(cos

⇒ (√3 + 1)(2 + 2i) = 4√2(cos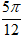
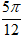
Lại có; 1 - i = √2.(cos(- 

Suy ra:
z = 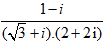
= 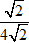

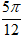

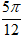
= 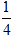
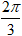
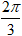
Chọn C.
Dạng 3: Công thức Moa-vro
1. Phương pháp giải
* Công thức Moa- vro
Cho số nguyên dương n ta có;
[r(cosφ + i.sinφ)]n = rn(cos(nφ) + i.sin(nφ))
Khi r = 1 ta có:
(cosφ + i.sinφ)n = cos(nφ) + i.sin(nφ)
2. Ví dụ minh họa
Ví dụ 1: Viết số phức sau dưới dạng lượng giác: z = (√2 + √2i)10
A. 25(cos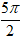
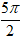
B. 210(cos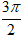
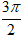
C. 25(cos(- 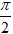
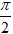
D. 210(cos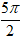
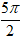
Lời giải:
Ta có: √2 + √2i = 2.(cos

Do đó,
z = (√2 + √2i)10 = [2.(cos

= 210(cos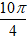
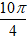
= 210.(cos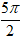
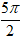
Chọn D.
Ví dụ 2: Viết số phức sau dưới dạng lượng giác z =
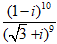
A. 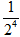
B. 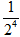
C. 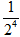
D. 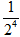
Lời giải:
* Ta có:
1 - i = √2(cos(- 

⇒ (1 - i)10
= √210.[cos(-10.

= 25[cos(- 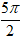
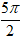
* Lại có:
√3 + i = 2(cos

⇒ (√3 + i)9 = 29.(cos9.

= 29.(cos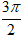
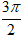
* Do đó,
z = 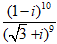
= 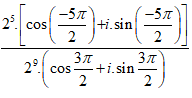
= 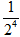
Chọn A.
Ví dụ 3: Cho số phức sau
(cos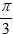
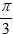
Tìm phần ảo của số phức.
A. 64 B. 128 C. 256 D. 32
Lời giải:
Ta có: 1 + √3i = 2.(cos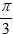
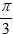
(cos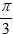
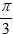
= (cos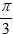
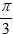
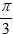
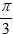
= 27(cos(- 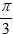
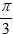
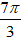
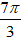
= 27[cos2π + isin2π]i = 27i
Vậy phần ảo bằng 27 = 128.
Chọn B.
Ví dụ 4: Tính số phức sau:
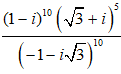
A. 1+ i B. 2 + 2i C. – 1 D. 2i
Lời giải:
* Ta có: 1 - i = √2.(cos(- 

√3 + i = 2(cos

-1 - i√3 = 2(cos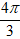
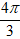
* Do đó:
z = 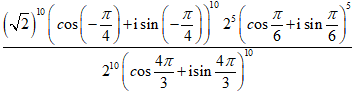
= 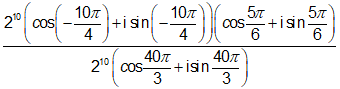
= 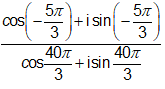
= cos(-15π) + i.sin(-15π) = -1
Chọn C.
Ví dụ 5: Cho số phức z = 1 - cos

A. (2sin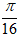
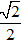
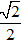
B. (2sin
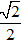
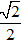
C. (2sin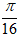


D. (2sin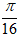


Lời giải:
Ta có:
z = 2sin2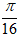
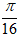
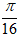
= 2sin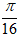
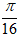
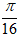
= 2sin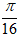
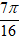
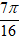
⇒ z2012
= (2sin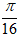
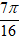
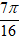
= (2sin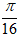
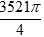
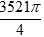
= (2sin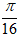


= (2sin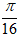
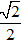
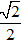
Chọn A.
Dạng 4: Ứng dụng công thức Moa- vro
2. Ví dụ minh họa
Ví dụ 1: Giải phương trình:
z5 + z4 + z3 + z2 + z + 1 = 0?
A. z = -1; z = 



z = 



B. z = -1; z = 1 + 





C. z = -1; z = 



z = 

D. z = -1; z = 1 + √3i ; z = - 

z = - 

Lời giải:
Ta có: z5 + z4 + z3 + z2 + z + 1 = 0
⇔ z4.(z + 1) + z2.(z + 1) + (z+ 1) = 0
⇔ ( z+1).(z4 + z2 + 1) = 0
⇔ 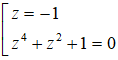
Xét phương trình: z4 + z2 + 1 = 0 (*)
Đặt t = z2, khi đó phương trình (*) trở thành: t2 + t + 1 = 0 (**)
Có ∆ = 12 – 4.1.1 = - 3.
Khi đó, (**) có hai nghiệm phức là:
t =
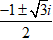
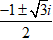
⇔ 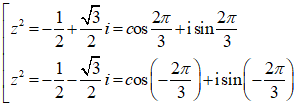
Từ z2 = cos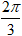
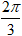
⇒ 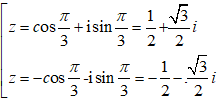
Từ z2 = cos(- 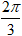
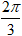
⇒ 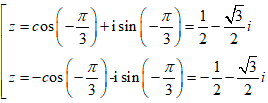
Vậy phương trình đã cho có tất cả 5 nghiệm:
z = -1; z = 



z = 



Chọn A.
Ví dụ 2: Giải phương trình z6 + 64= 0 ?
A. √3 ± 2i; ±2i; -√3 ± i
B. √3 ± i; ±2i; -√3 ± i
C. √3 ± i; ±2i; -√3 ± 2i
D. 1 ± √3; ±2i; 1 ± √3
Lời giải:
Ta có: : z6 + 64 = 0 ⇔ z6 = - 64.
+ Giả sử z = x + yi = r(cosφ + isinφ);
(x,y ∈ R)
⇒ z6 = r6.(cos6φ + isin6φ) (1)
+ Ta có: -64 = 64(cosπ + isinπ) và z6 = -64 (2)
Từ (1), (2)
⇒ r6(cos6φ + isin6φ)= 64(cosπ + isinπ)
⇒ r6 = 64 ⇒ r = 2( vì r > 0).
Và cos6φ + isin6φ = cosπ + isinπ
⇒ 6φ = π +2kπ (k ∈ Z)
⇒ φ = 

Với k = 0 ⇒ z1 = 2(cos

Với k = -1
⇒ z2 = 2(cos(- 

Với k = 1 ⇒ z3 = 2(cos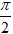
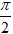
Với k = -2
⇒ z4 = 2(cos(- 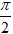
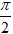
Với k = -3
⇒ z5 = 2(cos(- 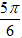
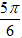
Với k = 4
⇒ z6 = 2(cos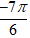
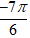
Vậy phương trình đã cho có 6 nghiệm là: √3 ± i; ±2i; -√3 ± i
Chọn B ..
Ví dụ 3: Gọi S là tập hợp các số nguyên dương n và n ∈ [1; 10] sao cho số phức z = (1 + i√3)n là số thực. Số phần tử của tập S là?
A. 2 B.3 C. 4 D. 5
Lời giải:
Ta có: 1 + i√3 = 2(cos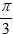
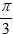
⇒ z = 2n(cos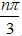
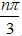
Để z ∈ R ⇒ 2n.sin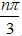
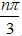
⇒ n chia hết cho 3, mà n nguyên dương
n ∈ [1;10]
⇒ n ∈ {3;6;9}.
Do đó, tập S có ba phần tử.
Chọn B.
Ví dụ 4: Tìm số phức z sao cho z5 và
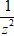
A. z1 = 1; z2 = 



B. z1 = - 1; z2 = 



C. z1 = 1; z2 = - 



D. Đáp án khác.
Lời giải:
* Gọi dạng lượng giác của số phức z là:
z = r(cosφ + i.sinφ)
⇒ z5 = r5(cos5φ + i.sin5φ);
z2 = r2(cos2φ + i.sin2φ)
⇒ 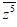
= r5(cos(-5φ) + i.sin(-5φ))
* 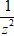
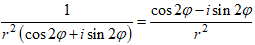
= 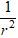
* Do đó z5 và 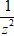
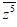
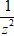
Hay là: r5(cos(-5φ) + i.sin(-5φ))
= 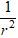
⇔ 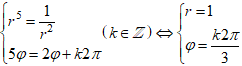
⇒ z = cos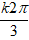
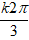
Vì φ ∈ [0; 2π] nên k ∈ {0; 1; 2}
Vậy số phức cần tìm là
z = cos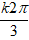
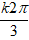
Hay z1 = 1; z2 = - 



Chọn C.
Ví dụ 5: Tính S1 = 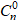
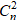
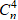
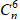
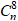
A. (√2)ncos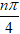
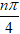
C. (√2)ncos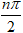
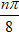
Lời giải:
Xét khai triển nhị thức Newton:
(1 + i)n = 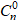
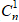
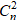
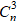
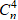
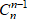
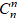
Vì ik = 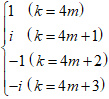
(1 + i)n = 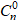
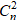
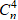
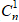
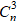
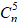
Mặt khác, theo công thức Moivre thì:
(1 + i)n = (√2)n(cos

= (√2)n(cos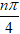
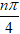
Từ (1) và (2) ta suy ra:
S1 = 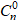
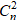
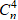
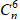
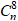
= (√2)ncos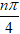
Chọn A

