Bài tập số phức cơ bản trong đề thi Đại học có lời giải (6 dạng) - Toán lớp 12

---

Bài tập số phức cơ bản trong đề thi Đại học có lời giải (6 dạng)

Với Bài tập số phức cơ bản trong đề thi Đại học có lời giải (6 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1: Cộng, trừ số phức

1. Phương pháp giải

Cho hai số phức z₁ = a + bi và z₂ = c + di thì:

    • Phép cộng số phức:
z₁ + z₂ = (a + c) + (b + d)i

   • Phép trừ số phức: z₁ – z₂ = ( a- c) + ( b – d) i

2. Ví dụ minh họa

Ví dụ 1: Cho hai số phức z₁ = 1 + 10i và
z₂ = 9 – 2i. Số phức z = z₁ + z₂ có z₁ có phần thực là:

A. 8    B. 10    C. 12    D. 14

Lời giải:

Ta có:
z = z₁ + z₂ = (1 + 10i) + ( 9 – 2i) = 10 + 8i.

Do đó, phần thực của số phức z là 10.

Đáp án: B

Ví dụ 2:Hãy tính số phức z. Biết rằng:
z = 10i – ( 2 + 2i).i

A. z = 2 + 8i    B. z = 8 - 2i

C. z = 8 + 2i    D. z = 2 - 8i

Lời giải:

Ta có
z = 10i - (2 + 2i).i = 10i – 2i + 2 = 2 + 8i

Đáp án: A

Ví dụ 3: Cho hai số phức z = -2 + 3yi;
z’ = ( x + 1)- 4i với x,y ∈ R .
Tìm x; y để z + i= z’ + 2

A. x = -5; y = 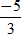   B. x = 5; y = 2

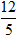
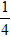
C. x = 2; y =    D. x = ; y = -2

Lời giải:

Để z + i = z’ + 2
⇔ - 2 + 3yi + i = ( x + 1) – 4i + 2

⇔ - 2 + (3y + 1).i = ( x + 3)- 4i

Do đó ta có hệ phương trình :
⇔

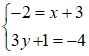
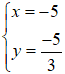
Đáp án: A

Ví dụ 4: Cho z₁ = a + 8i ,z₂ = 6 – 3i và
z₃ = 10 + bi ( a,b ∈ R ). Tìm a, b để z₁ + z₂ = z₃

A. a = 2; b = 5    B. a = 1; b = -5

C. a = 4; b = 5    D. a = 3; b = 1

Lời giải:

Ta có: z₁ + z₂ = z₃
nên (a + 8i) + ( 6 – 3i) =10 + bi

⇔ ( a + 6) + 5i = 10 + bi

⇔ ⇔

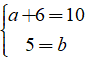
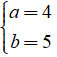
Vậy a = 4; b= 5.

Đáp án: C

Ví dụ 5: Số nào trong các số phức sau là số thuần ảo?

A. (√2 + i) - (1 + √2i)    B. ( 8 + 2i) + (- 8 + 2i)

C. ( - 3 + i) – ( 3 - i)    D. (10 + 3i) – ( -10 – 3i)

Lời giải:

Ta xét các phương án:

* (√2 + i) - (1 + √2i)= (√2 - 1) - (1 - √2) không là số thuần ảo.

* (8 + 2i) + (- 8 + 2i) = 4i là số thuần ảo.

* (-3 + i) – (3- i) = - 3 + i – 3 + i= - 6 + 2i không là số thuần ảo.

* (10 + 3i) – ( -10 – 3i) = 10 + 3i + 10 + 3i
= 20 + 6i không là số thuần ảo.

Đáp án: B

Dạng 2: Nhân, chia hai số phức

1. Phương pháp giải

Phép nhân số phức:
z₁.z₂ = ( ac – bd) + ( ad + bc). i

Phép chia số phức:

• Số phức nghịch đảo của z = a + bi ≠ 0
là = =

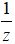
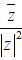
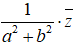
• Thực hiện phép chia là nhân cả tử và mẫu với số phức liên hợp của a + bi

=
= +

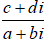
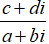
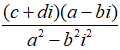
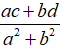
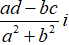
2. Ví dụ minh họa

Ví dụ 1: Tính giá trị của P= i¹⁰⁵ + i²³ + i²⁰ – i³⁴

A. 1    B. -2    C. 2    D. 5

Lời giải:

Ta có : i² = -1 ⇒ i⁴ = 1.

    Do đó, P = i¹⁰⁵ + i²³ + i²⁰ – i³⁴

                    = i^{104 + 1} + i^{20 + 3} + i^4.5 – i^{4.8 + 2}

                    = i. i^4.26 + i².i.i^4.5 + 1- i². i^4.8

             = i. 1 + (-1).i.1 + 1 - (-1).1 = 2

Đáp án: C

Ví dụ 2: Tìm số phức z = [(1 + 5i) - (1 + 3i)]²⁰⁰⁷.

A. z= - 8²⁰⁰⁷.i    B. z= -8²⁰⁰⁷.i

C. z= -2²⁰⁰⁷    D. z= -2²⁰⁰⁷.i

Lời giải:

z = [(1 + 5i) - (1 + 3i)]²⁰⁰⁷ ⇔ z = [2i]²⁰⁰⁷

⇔ z = 2²⁰⁰⁷i²⁰⁰⁷
⇔ z = 2 ²⁰⁰⁷ i^4.501.i².i=2 ²⁰⁰⁷ (-i)

( Vì i² = -1 nên i⁴ =1)

Đáp án: D

Ví dụ 3: Gía trị của biểu thức
A = + bằng

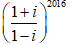
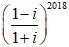
A. 1 + i    B. 2    C. 0    D. -2

Lời giải:

Ta có:

= = = = i

= = = = - i ;

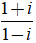
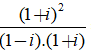
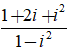
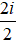
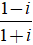
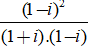
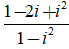
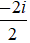
Suy ra:

A = +
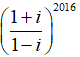
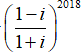
= i²⁰¹⁶ + (-i)²⁰¹⁸

= (i²)¹⁰⁰⁸ + (i²)¹⁰⁰⁹ = (-1)¹⁰⁰⁸ + (-1)¹⁰⁰⁹
= 1-1 = 0

Đáp án: C

Ví dụ 4: Cho P= 1 + i + i² + i³ + ... + i²⁰¹⁷. Tính P?

A. P= i + 1    B. P= 1    C. P= i    D. P= 2i

Lời giải:

Ta có;

P= 1 + i + i² + i³ + ... + i²⁰¹⁷

iP= i + i² + i³ + ... + i²⁰¹⁸

⇒ P - iP = 1 - i²⁰¹⁸

⇒ P = = =
= = = 1 + i

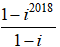
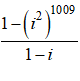
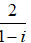
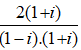
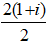
Đáp án: A

Ví dụ 5: Cho A = 1 + i² + i⁴ + .. + i^4k-2 + i^4k với k là số nguyên dương. Tính A?

A. A = 2ki    B. A = 2k    C. A = 0    D. A = 1

Lời giải:

Do A là tổng của một cấp số nhân (gồm 2k + 1 số hạng) với số hạng đầu u₁ = 1, công bội q= i².

Suy ra

A = 1 + i² + i⁴ + .. + i^4k-2 + i^4k

= =
= = 1

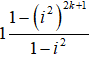
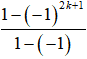
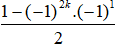
Đáp án: D

Dạng 3: Tìm số phức liên hợp

1. Phương pháp giải

Cho số phức z= a + bi,( a,b ∈ R). Khi đó, số phức liên hợp với số phức z là: z− = a - bi

2. Ví dụ minh họa

Ví dụ 1: Tìm số phức liên hợp của số phức
z = ( 3- 2i). (2 + 3i)

A. z− = -5i    B. z− = 12 -5i

C. z− = 12 + 5i    D. z− = 3 + 2i

Lời giải:

Ta có: z = (3 - 2i).(2 + 3i) = 6 + 9i – 4i + 6

⇔ z = 12 + 5i Do đó, số phức liên hợp với số phức z là z− = 12 -5i

Đáp án: B

Ví dụ 2: Cho số phức z = 5 – 3i. Tính 1 + z− + (z− )² ta được kết quả:

A. – 22 + 33i.    B. 22 + 33i.

C. 22 - 33i.    D. -22 - 33i.

Lời giải:

Ta có z = 5 - 3i ⇒ z− = 5 + 3i

Suy ra : 1 + z− + (z− )² = 1 + (5 + 3i) + (5 + 3i)²
= (6 + 3i) + (25 + 30i - 9) = 22 + 33i

Đáp án: B

Ví dụ 3: Cho số phức z = 4 - 3i. Tìm số phức liên hợp của số phức ω = 2z− + z².

A. ω− = 15 - 18i    B. ω− = 16 + 18i

C. ω− = 15 + 16i    D. ω− = 15 + 18i

Lời giải:

Ta có z = 4 - 3i nên số phức liên hợp với số phức z là : z− = 4 + 3i

Theo đầu bài :
ω = 2z− + z² = 2. (4 + 3i) + ( 4-3i)²

⇔ ω = 8 + 6i + ( 16 – 24i + 9i²) = 15 – 18i

Vậy ω = 15 – 18i

Vậy số phức liên hợp của ω là
ω− = 15 + 18i

Đáp án: D

Ví dụ 4: Cho số phức z thỏa
(1 + 3i) z - (2 + 5i) = (2 + i) z. Tìm số phức liên hợp của số phức z.

A. z− = +    B. z− = - +

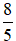
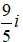
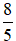
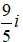
C. z− = -    D. z− = - -

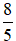
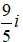
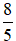
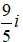
Lời giải:

Theo giả thiết ta có:

(1 + 3i)z-(2 + 5i) = (2 + i)z

⇔(1 + 3i-2-i)z = 2 + 5i⇔(-1 + 2i)z = 2 + 5i

⇔z = = +

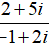
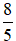
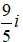
Đáp án: A

Ví dụ 5: Tìm số phức z, biết z + 2iz− + 4 = i

A. z = 2- 3i    B. z = - 3 + 2i

C. z = - 2 + 3i    D. z = 3 - 2i

Lời giải:

Gọi số phức z cần tìm là
z = a + bi ( a,b ∈ R)

Số phức liên hợp với số phức z là :
z− = a - bi

Theo giả thiết: z + 2iz− + 4 = i

⇒ a + bi + 2i(a - bi) + 4 = i

⇔ a + bi + 2ai + 2b + 4-i = 0

⇔(a + 2b + 4) + (b + 2a-1)i = 0

⇔ ⇔

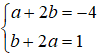
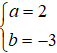
Suy ra z = 2- 3i

Đáp án: A

Dạng 4: Môđun của số phức

1. Phương pháp giải

* Cho số phức z = a + bi, ( a,b ∈ R). Khi đó mô đun của số phức z kí hiệu là : | z| và :
| z| =

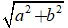
* Nhận xét : |z| ≥ 0 và |z| = 0 ⇔ z = 0 .

2. Ví dụ minh họa

Ví dụ 1: Tính môđun của số phức z = 6 – 8i

A. 10    B. 2    C. -2    D. 80

Lời giải:

Môđun của số phức z = 6 – 8i là:
| z| = = 10

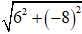
Đáp án: A

Ví dụ 2: Tìm số phức z, biết | z| = √5 , phần thực bằng 2 lần phần ảo và phần thực dương

A. z = 2 + i    B. z = 1 + 2i

C. z = +    D. z = +

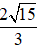
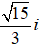
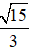
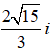
Lời giải:

Cho số phức z = a + bi, ( a,b ∈ R) và a > 0

Do phần thực bằng 2 lần phần ảo nên :
a = 2b (1).

mà | z| = √5 ⇔ = √5
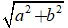
⇔ a² + b² = 5 (2)

Từ (1) và (2) ta có hệ phương trình :

⇔

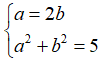
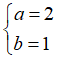
Vậy số phức cần tìm là z = 2 + i.

Đáp án: A

Ví dụ 3: Cho số phức z có phần thực là số nguyên và z thỏa mãn: | z| - 2z− = -7 + 3i + z . Tính môđun của số phức: ω = 1 - z + z²

A. |ω| = √37    B. |ω| = √457

C. |ω| = √425    D. |ω| = 457

Lời giải:

Gọi số phức cần tìm là z = a + bi, ( a,b ∈ R)

Số phức liên hợp của số phức z là : z− = a - bi và | z| =

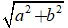
Theo giả thiết ta có: | z| - 2z− = -7 + 3i + z

⇔ - 2(a - bi) = -7 + 3i + a + bi

⇔
⇔ ⇔

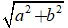
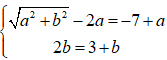
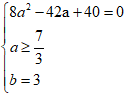
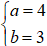
vậy z = 4 + 3i
⇒ ω = 1-(4 + 3i) + (4 + 3i)² = 4 + 21i

⇒ |ω| = = √457

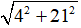
Đáp án: B

Ví dụ 4: Cho hai số phức z₁ và z₂ thỏa Cho hai số phức z₁ và z₂ thỏa |z₁ | = |z₂ | = 1;
|z₁ + z₂ |=√3. Tính |z₁ - z₂ |

A. √3-1    B. 0    C. 1    D. -1

Lời giải:

Ta có :

3 =|z₁ + z₂ |² = (z₁ + z₂ )( z− ₁ + z− ₂ )

⇒z₁ z− ₂ + z₂ z− ₁ + z₁ z− ₁ + z₂ z− ₂ = 3

⇒z₁ z− ₂ + z₂ z− ₁ = 1

Vì |z₁| = |z₂| = 1 nên z₁. z₁− = 1 ; z₂. z₂− = 1

Khi đó:

|z₁ - z₂|² = (z₁ - z₂)(z₁− - z₂− )
= |z₁|² + |z₂|² - (z₁ z₂− + z₂ z₁− ) = 1

Đáp án: C

Ví dụ 5: Cho số phức z thỏa mãn | z + 3| = 5 và | z- 2i|= |z – 2 - 2i|. Tính |z|.

A. |z| = 5    B. |z| = √5

C. |z| = 2    D. |z| = √10

Lời giải:

Gọi số phức z cần tìm là
z = a + bi ( a,b ∈ R)

Ta có:

|z + 3| = 5⇔|a + bi + 3| = 5
⇔(a + 3)² + b² = 25 (*)

|z-2i| = |z-2-2i|
⇔|a + bi-2i| = |a + bi-2-2i|

⇔a² + (b-2)² = (a - 2)² + (b - 2)²

⇔a² = (a-2)²

⇔

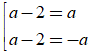
Thế a = 1 vào (*) ta được 16 + b² = 25
⇒ b² = 9

Do đó, môdun của z là:
|z| = = √10

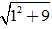
Đáp án: D

Dạng 5: Tìm số phức thỏa mãn điều kiện T

1. Phương pháp giải

Để tìm được số phức thỏa mãn điều kiện T, ta cần linh hoạt các phép toán của số phức, tính môdun số phức, số phức liên hợp...

2. Ví dụ minh họa

Ví dụ 1: Cho số phức z = 2m + ( m + 2)i, (m∈ R) . Tìm z biết rằng z² là một số phức có phần thực bằng - 5.

A. Không có số phức cần tìm

B. z = 2 + 3i , z = +

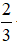
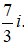
C. z = 4 + 2√3 + (4 + √3)i; z = 4 - 2√3 + (4 - √3)i

D. z = 2i, z = -18 – 7i

Lời giải:

Ta có :

z² = 4m² + 2m(m + 2)i + [(m + 2)i]²
= 3m² + 2m(m + 2)i-4m-4

Do z² là số phức có phần thực bằng -5 nên ta có:

⇒ 3m² - 4m - 4 = -5 ⇔ 3m² - 4m + 1 = 0 ⇔ m = 1 ; m = 1/3

Vậy có hai số phức thỏa mãn là z₁ = 2 + 3i và z₂ = +

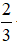
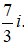
Đáp án: B

Ví dụ 2: Cho số phức z = m + (m-1)i; (m∈ R) và số phức z' = 2n + (2-3n)i (n∈R) .Tìm m và n biết rằng z - z’= 1 + 7i

A. m = ; n =    B. m = ; n =

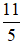
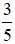
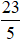
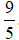
C. m = -9, n = -5    D. m = -13, n = - 7

Lời giải:

Ta có:
z - z’
= [ m + ( m - 1).i] – [2n + (2- 3n).i]
= (m- 2n) + ( m + 3n – 3). I

Theo giả thiết z- z’ = 1 + 7i nên ta có:

( m- 2n) + (m + 3n – 3).i = 1 + 7i .

Từ đó ta có hệ phương trình sau:

⇔
⇔

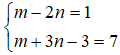
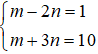
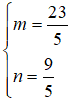
Đáp án: B

Ví dụ 3: Tìm số phức z = x + yi, ( x, y ∈ R) thỏa mãn z + 3x = 2z− - 3i . Tìm |z|

A. |z| = 1    B. |z| = 2

C. |z| = √2    D. |z| = √3

Lời giải:

Vì z + 3x = 2z− - 3i
⇔ x + yi + 3x = 2(x - yi) - 3i
⇔ 4x + yi = 2x - (2y + 3)i

⇔ ⇔

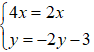
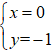
Do đó, số phức thỏa mãn đầu bài là
z = - i và |z| = 1

Đáp án: A

Ví dụ 4: Có bao nhiêu số phức z có phần ảo gấp ba lần phần thực, đồng thời
|z− | =

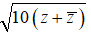
A. 0    B. 1    C. 2    D. 3

Lời giải:

Gọi số phức cần tìm là z = a + bi, ( a,b ∈ R)

Do số phức z có phần ảo gấp ba lần phần thực nên b = 3a

⇒ Số phức cần tìm có dạng: z = a + 3ai

Số phức liên hợp của số phức z là:
z− = a - 3ai

Theo giả thiết ta có:
|z−| =
⇔ =

⇔ =
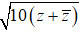
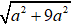
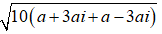
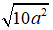
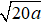
⇔ 10a² = 20a ⇔

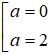
Với a = 0 thì z = 0.

Với a = 2 thì z = 2 + 6i

Vậy có hai số phức thỏa mãn là z = 0 hoặc z = 2 + 6i

Đáp án: C

Ví dụ 5: Trong mặt phẳng Oxy cho điểm A là điểm biểu diễn của số phức z= 1 + 2i, B là điểm thuộc đường thẳng y=2 sao cho tam giác OAB cân tại O. Tìm số z biểu diễn B.

A. z = 1 + 2i.    B. z = -1 + 2i.

C. z = 3 + 2i, z = -3 + 2i.    D. z = - 1 + 2i, z = 1 + 2i.

Lời giải:

Ta có, điểm A biểu diễn số phức z = 1 + 2i nên tọa độ A( 1; 2) .

Do điểm B nằm trên đường thẳng y = 2 nên tọa độ B(x, 2); ( x ≠ 1 )

Để tam giác OAB cân tại O khi và chỉ khi OA = OB.

⇔ = ⇔ x² + 4 = 5
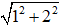
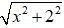
⇔ x² = 1 ⇔

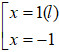
Suy ra, tọa độ B (-1; 2). Do đó,số phức biểu diễn B là z = -1 + 2i

Đáp án: B

Dạng 6: Giải phương trình bậc nhất trên tập số phức

1. Phương pháp giải

Cho phương trình az + b= 0 (a ≠ 0 ) a, b là hai số phức ⇔ az = -b ⇔ z =

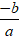
Sau đó, thực hiện phép chia số phức để tìm ra z.

2. Ví dụ minh họa

Ví dụ 1:Cho số phức z thỏa mãn:
(2 + i)z + 2 – i= 0. Tìm phần thực của số phức.

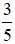
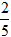
A. -    B. -3    C. 5    D.

Lời giải:

Ta có: (2 + i ).z + 2- i = 0 ⇔ ( 2 + i)z = - 2 + i

⇔ z = =

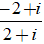
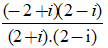
⇔ z = =

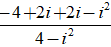
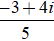
Do đó, phần thực của số phức cần tìm là -

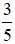
Đáp án: A

Ví dụ 2: Giải phương trình iz + 3- 2i = 1 + i

A. z = 2 + 3i    B. z = 1- 3i

C. z = 3 + 2i    D. z = 2 + 2i

Lời giải:

Ta có: iz + 3 – 2i = 1 + i

⇔ iz = 1 + i- 3 + 2i

⇔ iz = -2 + 3i

⇔ z = = = 3 + 2i

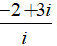
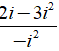
Đáp án: C

Ví dụ 3: Giải phương trình:
( 2 + 4i)z + ( 4 - 2i)z + 2- 2i = 0

A. z =    B. z =

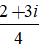
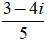
C. z =    D. z =

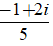
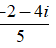
Lời giải:

Ta có: ( 2 + 4i).z + (4 –2 i). z + 2- 2i = 0

⇔( 2 + 4i + 4 – 2i)z = - 2 + 2i
⇔ (6 + 2i). z = - 2 + 2i

⇔ z = =
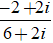
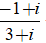
⇔z =

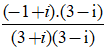
⇔z = = =

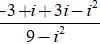
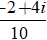
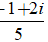
Đáp án: C

Ví dụ 4: Giải phương trình (1 + 2i)z + = 0

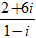
A. z =    B. z =

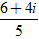
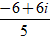
C. z =    D. z =

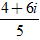
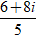
Lời giải:

Ta có:

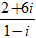
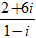
(1 + 2i)z + = 0 ⇔ (1 + 2i)z =

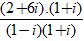
⇔ (1 + 2i)z =

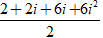
⇔ (1 + 2i)z =

⇔ (1 + 2i)z = ⇔ (1 + 2i)z = -2 + 4i

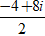
⇔ z = =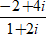

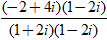
⇔ z =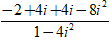

⇔ z =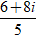

Đáp án: D