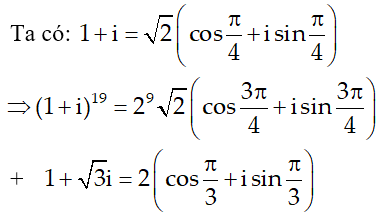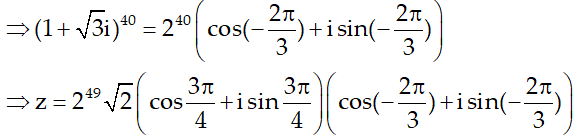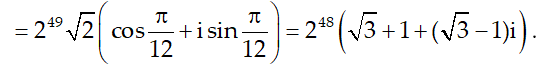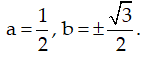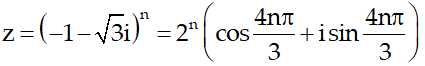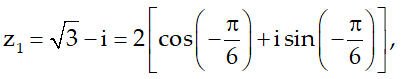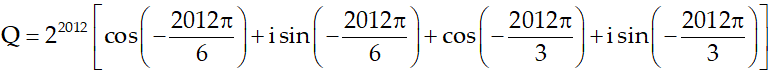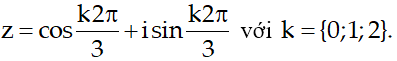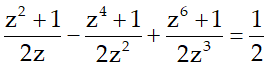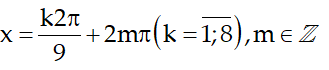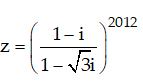Cách viết số phức dưới dạng lượng giác cực hay, chi tiết - Toán lớp 12

---

Cách viết số phức dưới dạng lượng giác cực hay, chi tiết

Với Cách viết số phức dưới dạng lượng giác cực hay, chi tiết Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập viết số phức dưới dạng lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Cần chú ý hai công thức quan trọng sau

Công thức 1:

(cos x + i sin x). (cosy + i sin y) = cos(x + y) + isin(x +y)

Công thức 2 : (cos X + i sin x)n = cos nx + i sin nx

Số phức z = a + bi ta có: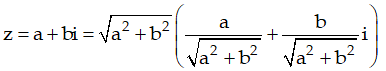

= |z| (cosφ +i sinφ) = r(cosφ + isinφ)

Với r = |z| và góc φ được gọi là argument của z, ký hiệu là arg(z) . Ngược với phép luỹ thừa ta có phép khai căn

Ví dụ minh họa

Ví dụ 1:Viết số phức z = -2 + 2i dưới dạng lượng giác?

Hướng dẫn:

Ta có:

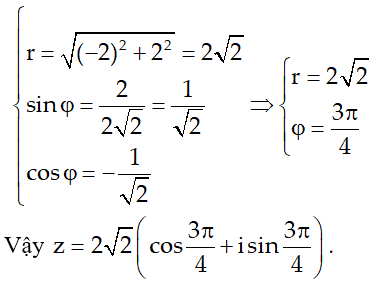
Ví dụ 2:Viết các số phức z = √6 - √2i dưới dạng lượng giác . Từ đó hãy viết dạng đại số của z²⁰¹²

Hướng dẫn:

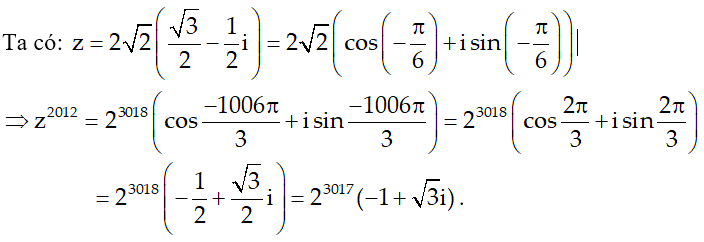
Ví dụ 3:Viết các số phức 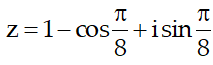dưới dạng lượng giác . Từ đó hãy viết dạng đại số của z²⁰¹²

Hướng dẫn:

Ta có:

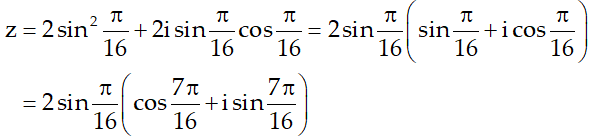
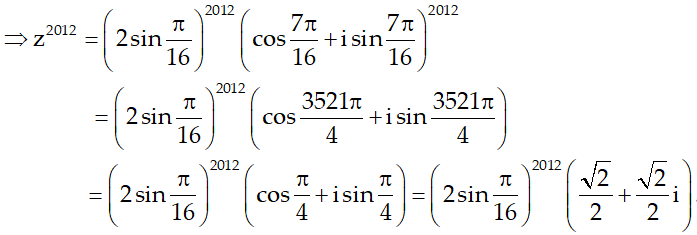
Ví dụ 4:Tìm các số nguyên dương n để số phức z = (1-i)ⁿ là số thực?

Hướng dẫn:

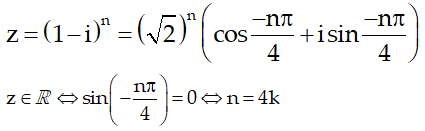
Ví dụ 5: Cho số phức z thỏa mãn 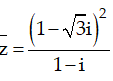. Tìm môđun của số phức z + iz

Hướng dẫn:

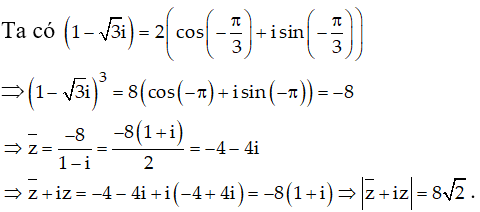
Ví dụ 6:. Tìm phần thực và phần ảo của số phức sau: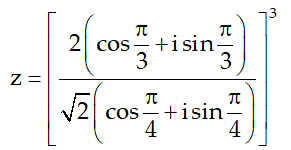

Hướng dẫn:

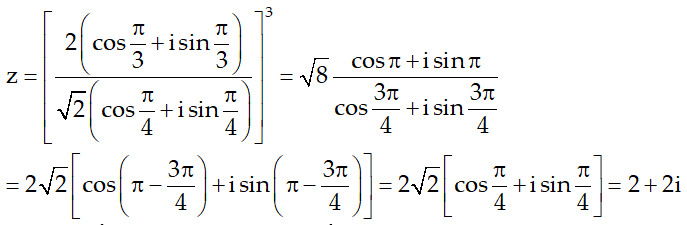
Vậy phần thực của z là 2 và phần ảo của z là 2.

Ví dụ 7:Tính A = (1+i)¹² + (1-i)¹²

Hướng dẫn:

Ta có:

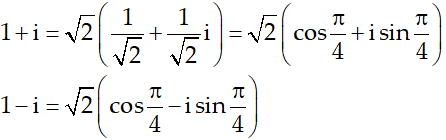
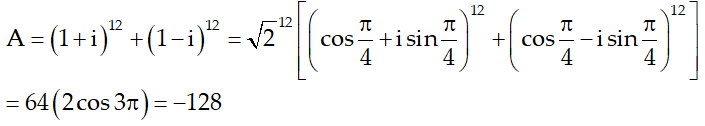
Ví dụ 8:Cho số phức z₁; z₂ thỏa mãn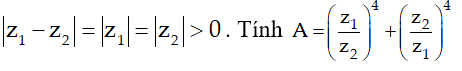

Hướng dẫn:

Đặt 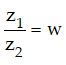và w = a + bi ; khi đó:

|z₁ - z₂| = |z₁| = |z₂| > 0 tương đương với |w - 1| = |w| = 1 tức (a-1)² + b² = a² + b² = 1 hay

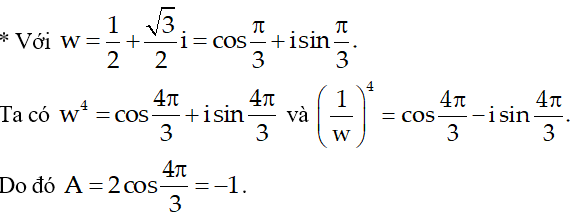
B. Bài tập vận dụng

Câu 1:Tìm các số nguyên dương n để số phức z = (√3 + i)ⁿ là số thực ?

Lời giải:

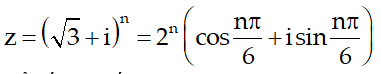
Để số z là số thực khi

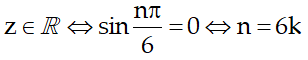
Câu 2:Tìm các số nguyên dương n để số phức z=(-1 - √3i)²là số ảo?

Lời giải:

Ta có:

Để z là số ảo thì n phải thỏa mãn:

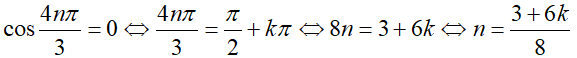
Do 3 + 6k là số lẻ nên (3 + 6k) không chia hết cho 8.

Vậy không tồn tại n để z là số ảo.

Câu 3:Gọi z₁; z₂ là nghiệm của phương trình: z² - (1 + √3)(1 -i)z - 4i = 0 . Tính giá trị biểu thức Q = z₁²⁰¹² + z₂²⁰¹²

Lời giải:

Phương trình: z² - (1 + √3)(1 -i)z - 4i = 0 có biệt số Δ = 2i(4-2√3)

Dễ thấy 4-2√3 = (√ - 1)² . 2i = (i + 1)² . Khi đó Δ = [(√ - 1)(i + 1)]²

Suy ra phương trình cho có 2 nghiệm z₁ = √3 - i , z₂ = 1 - i√3

Mặt khác

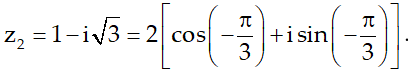
Khi đó :

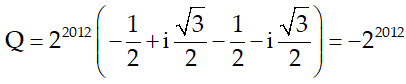
Câu 4: Tìm số phức z sao cho z⁵ và 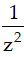là hai số phức liên hợp.

Lời giải:

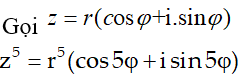
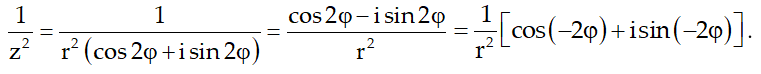
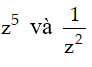
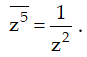
Do đó là hai số phức liên hợp khi và chỉ khi

Hay là: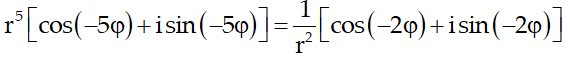

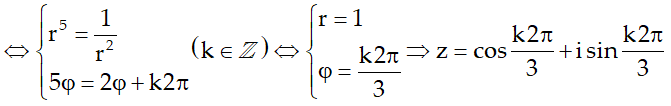
Vì φ ∈ (0;2r) nên k = {0;1;2}.

Vậy số phức cần tìm là

Câu 5:Giải phương trình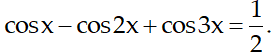

Lời giải:

Đặt z = cosx + i.sinx thế thì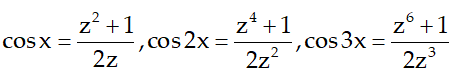

Phương trình cho trở thành:

Hay z⁶ - z⁵ + z⁴ - z³ + z² - z = 0

Vì z = 1 không là nghiệm phương trình, nên ta có:

(*) <=> (z + 1)(z⁶ - z⁵ + z⁴ - z³ + z² - z + 1) = 0 <=> z⁷ + 1 = 0

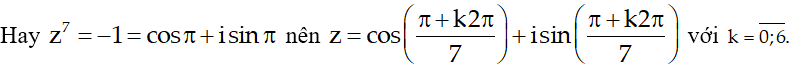
Vì z ≠ 1 nên không nhận giá trị k = 3

Vậy, phương trình cho có nghiệm:

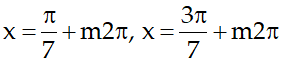
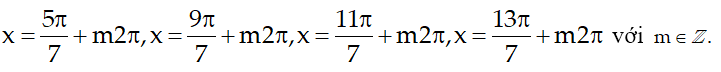
Câu 6:Giải phương trình : cosx + cos3x + cos5x + cos7x + cos9x =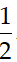

Lời giải:

Ta có cosx = ± 1 không là nghiệm của phương trình.

Đặt z = cosx + i.sinx với x ∈ (0;2r)

Ta có z ≠ ±1,z^-1 = cosx - i sinx và:

2cosx = z + z^-1, 2cosnx = zⁿ + ^-n

Vậy phương trình đã cho trở thành:

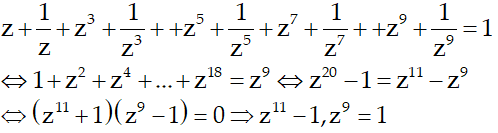
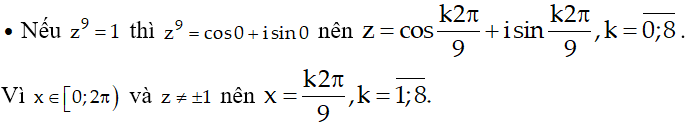
Do đó nghiệm của phương trình đã cho là

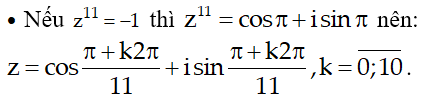
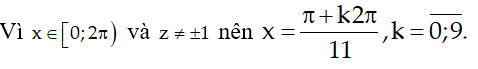
Suy ra nghiệm cần tìm là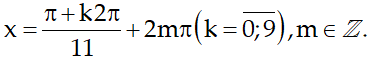

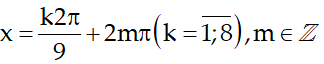
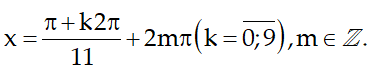
Vậy các nghiệm của phương trình là: và

Câu 7:Viết các số phức sau dưới dạng đại số

Lời giải:

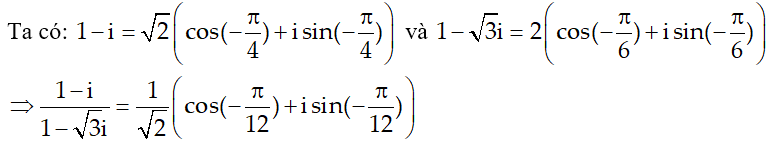
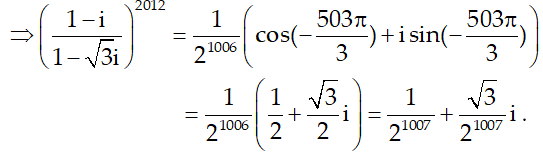
Câu 8: Viết các số phức sau dưới dạng đại số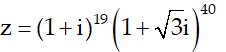

Lời giải: