Tìm tập hợp điểm biểu diễn số phức trong đề thi Đại học có lời giải (5 dạng) - Toán lớp 12

---

Tìm tập hợp điểm biểu diễn số phức trong đề thi Đại học có lời giải (5 dạng)

Với Tìm tập hợp điểm biểu diễn số phức trong đề thi Đại học có lời giải (5 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tập hợp điểm biểu diễn số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1: Điểm biểu diễn số phức

1. Phương pháp giải

+ Số phức z = a + bi, (a,b ∈ R) biểu diễn điểm M(a, b).

+ Ngược lại điểm M(a, b) biểu diễn số phức
z = a + bi.

2. Ví dụ minh họa

Ví dụ 1: Số phức z = (2 + 3i) + ( -10 + 8i) có điểm biểu diễn trên mặt phẳng tọa độ là:

A. ( 2; 4)    B. ( - 8; -10)    C. ( 10; - 7)    D. (- 8; 11)

Lời giải:

Ta có: z = (2 + 3i) + (- 10 + 8i)
= (2 – 10) + ( 3 + 8)i = - 8 + 11i.

Do đó điểm M( - 8; 11) biểu diễn số phức z đã cho.

Chọn D.

Ví dụ 2: Cho số phức z = ( 2 + 3i) .( 1- i). Điểm biểu diễn số phức liên hợp của z là

A. ( 5; -1)    B. ( 5; 1)    C. ( - 5; 1)    D. (-5; -1)

Lời giải:

Ta có: z= (2 + 3i).(1- i) = 2 – 2i + 3i - 3i²

= 2 + i + 3 = 5 + i.

⇒ z− = 5 - i

Điểm biểu diễn số phức liên hợp của z là M( 5; -1).

Chọn A.

Ví dụ 3: Cho A, B, C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức

z₁ = 1 + 2i, z₂ = -2 + 5i, z₃ = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là

A. – 1 + 7i.    B. 5 + i    C. 1 + 5i    D. 3 + 7i

Lời giải:

Ba điểm A, B và C lần lượt biểu diễn ba số phức z₁ = 1 + 2i, z₂ = -2 + 5i, z₃ = 2 + 4i nên tọa độ ba điểm này là: A( 1; 2), B( -2; 5), C(2; 4).

Gọi tọa độ điểm D(x, y).

Ta có : AB→(-3; 3); DC→(2 - x; 4 - y)

Để ABCD là hình bình hành thì :
AB→ = CD→

⇔

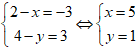
Do đó, tọa độ điêm D(5 ; 1). Số phức thỏa mãn là: z= 5 + i.

Chọn B.

Ví dụ 4: Cho 3 điểm A, B và C lần lượt biểu diễn cho các số phức z₁, z₂, z₃.
Biết |z₁| = |z₂| = |z₃| và z₁ + z₂ = 0 . Khi đó tam giác ABC là tam giác gì?

A. Tam giác ABC đều.

B. Tam giác ABC vuông tại C.

C. Tam giác ABC cân tại C .

D. Tam giác ABC vuông cân tại C.

Lời giải:

* Vì z₁ + z₂ = 0 nên z₁; z₂ là hai số phức đối nhau.

Do đó hai điểm A, B đối xứng qua gốc O( tức O là trung điểm của đoạn thẳng AB).

* Lại có |z₁| = |z₂| = |z₃| nên OA = OB = OC ⇔ CO = .

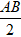
Vậy tam giác ABC có độ dài đường trung tuyến bằng một nửa cạnh huyền nên vuông tại C.

Chọn B.

Ví dụ 5: Cho hình bình hành ABCD. Bốn đỉnh A,B, C, D lần lượt biểu diễn các số phức
a = 2- 2i, b = -1 + i, c = 5 + mi, d = 8 + ( m - 3)i; . Tìm m sao cho ABCD là hình chữ nhật.

A. m = -1    B. m = 2    C. m = 7    D. m = 3

Lời giải:

* Do bốn điểm A, B, C và D lần lượt biểu diễn các số phức a = 2- 2i, b = - 1 + i,
c = 5 + mi và d = 8 + (m - 3)i nên ta có: A( 2; -2); B( - 1; 1); C( 5; m), D(8, m – 3)

* Do ABCD là hình bình hành nên để ABCD là hình chữ nhật khi và chỉ khi:

= 90⁰ ⇔ AB ⊥ BC

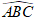
* Ta có: AB→(- 3; 3); BC→(6; m - 1)

Để AB vuông góc BC khi và chỉ khi:

AB→.BC→ = 0 ⇔ (-3).6 + 3(m - 1) = 0

⇔ -21m + 3 = 0 ⇔ m = 7

Chọn C

Dạng 2: Tập hợp điểm biểu diễn số phức là đường thẳng

1. Phương pháp giải

Cho số phức z = a + bi, (a,b ∈ R) . Gọi điểm M(a, b) là điểm biểu diễn số phức z.

Nếu tọa độ điểm M thỏa mãn A.a + B.b + C = 0 thì tập hợp điểm biểu diễn số phức z là đường thẳng Ax + By + C = 0

2. Ví dụ minh họa

Ví dụ 1: Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z + (1 + i)| = |z- 2i | là đường nào sau đây ?

A. x + 3y + 1 = 0    B. x + 3y - 1 =0

C. x- 2y + 1 = 0    D. 3x - y + 1 = 0

Lời giải:

* Gọi số phức z = x + yi, (x,y ∈ R) được biểu diễn bởi điểm M( x, y) trong mặt phẳng Oxy

* Theo giả thiết ta có:
|z + (1 + i)| = |z - 2i|

⇔ |x + yi + 1 + i|= | x + yi - 2i|

⇔ |(x + 1) + (y + 1)i| = | x + ( y - 2).i |

⇔

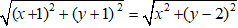
⇔ x² + 2x + 1 + y² + 2y + 1
= x² + y² – 4y + 4

⇔ 2x + 6y – 2 = 0 hay x + 3y – 1 = 0

Vậy tập hợp các điểm biểu diễn số phức z cần tìm là đường thẳng x + 3y – 1 = 0

Chọn B.

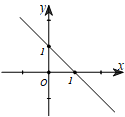
Ví dụ 2: Tập hợp các điểm biểu diễn của số phức z là đường thẳng ∆ như hình vẽ. Số phức z có môđun nhỏ nhất là:

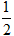
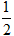
A. z = + i .    B. z = 1 + i.    C. z = 1    D. z = i

Lời giải:

* Đường thẳng ∆ đi qua A( 1; 0) và B(0; 1). Nên phương trình đoạn chắn của đường thẳng ∆ là:

= 1 ⇔ x + y - 1 = 0 .

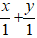
* Gọi điểm M biểu diễn số phức z. Do điểm M thuộc ∆ nên tọa độ M ( t; 1- t).

Suy ra, số phức z = t + (1- t).i

* Mô đun của số phức z là:

|z| =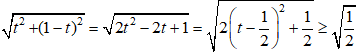

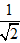
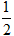
Do đó, min|z| = ⇔ t = .

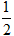
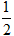
Vậy số phức z = + i .

Chọn A.

Ví dụ 3: Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: |z + z− + 3| = 4

A. Đường thẳng x = .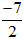

B. Đường thẳng x = .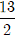

C. Đường thẳng x = .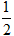

D. Đáp án khác.

Lời giải:

Gọi M(x, y) là điểm biểu diễn của số phức z = x + yi, (x,y ∈ R) trong mặt phẳng Oxy.

Số phức liên hợp với số phức z là z− = x - yi

Theo đề bài ta có:
|z + z− + 3| = 4
⇔ |x + yi + x - yi + 3| = 4
⇔ |2x + 3| = 4

⇔

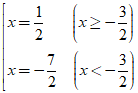
Vậy tập hợp điểm M(x, y) cần tìm là đường thẳng đường thẳng x = với
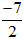
x < - và đường thẳng x = với x > -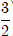

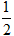
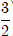
Chọn D.

Ví dụ 4: Cho số phức z = x + yi, (x,y ∈ R) .
Biết |z + 2 - i| = | - 2| . Tìm tập hợp các điểm biểu diễn số phức z.

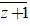
A. x + 3y – 1 = 0    B. x + y - 2 = 0

C. 3x – y + 2 = 0    D. x - 3y + 2 = 0

Lời giải:

Ta có: z = x + yi nên z + 1 = (x + 1) + yi

⇒ số phức liên hợp với z + 1 là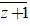
= (x + 1) - yi

Theo giả thiết ta có:
|z + 2 - i| = |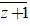 - 2|

|x + yi + 2 - i| = |( x + 1) – yi – 2|

⇔ | (x + 2) + ( y-1)i| = |( x -1) – yi|

⇔

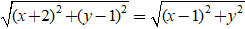
⇔ (x + 2)² + (y - 1)² = (x - 1)² + y²

⇔ x² + 4x + 4 + y² – 2y + 1
= x² – 2x + 1 + y²

⇔ 6x – 2y + 4 = 0 hay 3x – y + 2 = 0

Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng 3x – y + 2 = 0

Chọn C.

Dạng 3: Tập hợp điểm biểu diễn số phức là đường tròn

1. Phương pháp giải

* Cho số phức z = x + yi, (x,y ∈ R) . Gọi điểm M (x, y) biểu diễn số phức z trên mặt phẳng Oxy. Nếu x, y thỏa mãn: (x- a)² + ( y – b)² = R² thì tập hợp các điểm biểu diễn số phức z là đường tròn.

*Đường tròn (x- a)² + (y – b)² = R² là đường tròn có tâm I(a, b) và bán kính R.

2. Ví dụ minh họa

Ví dụ 1: Giả sử M là điểm trên mặt phẳng phức biểu diễn số phức z. Tập hợp các điểm M thoả mãn điều kiện sau đây: | z - 1 + i| = 2 là một đường tròn:

A. Có tâm (-1; -1) và bán kính là 2.

B. Có tâm (1; -1) và bán kính là √2

C. Có tâm (-1; 1) và bán kính là 2.

D. Có tâm (1; -1) và bán kính là 2

Lời giải:

Gọi số phức z = x + yi, (x,y ∈ R)

Theo giả thiết |z - 1 + i | = 2 nên

| x + yi -1 + i| = 2 ⇔ |(x- 1) + ( y + 1).i| = 2

⇔ = 2

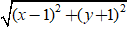
⇔ (x - 1)² + (y + 1)² = 4

Do đó, tập hợp các điểm M trên mặt phẳng toạ độ biểu diễn số phức z là đường tròn có tâm I(1; -1)và bán kính
R = 2.

Chọn D.

Ví dụ 2: Cho số phức z thỏa mãn |z + i| = 1. Biết rằng tập hợp các điểm biểu diễn các số phức w = z - 2i là một đường tròn. Tâm của đường tròn đó là:

A. I( 0;-2)    B. I( 0; -3).    C. I( 0; -6)    D. I( 0; 3)

Lời giải:

Ta có w = z - 2i ⇔ z = w + 2i .

Gọi w = x + yi (x,y ∈ R) .
Suy ra z = x + (2 + y).i.

Theo giả thiết, ta có

|z + i| = 1 ⇔ |x + (2 + y)i + i| = 1

⇔ |x + (3 + y)i| = 1 ⇔ 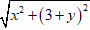= 1 ⇔ x² + (y + 3)² = 1 .

Vậy tập hợp các số phức w = z - 2i là đường tròn tâm I(0; -3).

Chọn B.

Ví dụ 3: Cho các số phức z thỏa mãn z = 3√5 . Biết rằng tập hợp các điểm biểu diễn các số phức w = (2 + i).z + i là một đường tròn. Tính bán kính R của đường tròn đó.

A. R = 4    B. R = 10    C. R = 3√5    D. R = 15

Lời giải:

Ta có w = x + yi (x,y ∈ R)

Do w = ( 2 + i).z + i nên

z =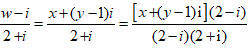

=

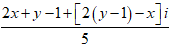
Theo giả thiết z = 3√5

⇒ |z|² =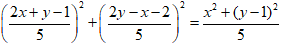

= 45

⇔ x² + ( y - 1)² = 225

Vậy tập hợp các điểm biểu diễn số phức w là đường tròn tâm I( 0; 1) và bán kính
R = 15.

Chọn D.

Ví dụ 4: Cho số phức z thỏa mãn |z - 2| = 2. Biết rằng tập hợp các điểm biểu diễn các số phức w = (1 - i)z + i là một đường tròn. Tính bán kính r của đường tròn đó

A. r = 2√2    B. r = 4    C. r = √2    D. r = 2

Lời giải:

Ta có: w = (1 – i).z + i nên z = .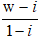

Gọi số phức w = x + yi, (x,y ∈ R) .

⇒ z = .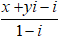

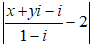
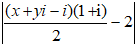
Ta có: | z- 2 |= 2 ⇒ = 2
⇔ = 2

⇔ | x + xi + yi - y – i + 1 – 4| = 4

⇔ | ( x – y – 3) + ( x + y – 1)i| = 4

⇔ ( x- y – 3)² + (x + y – 1)² = 16

⇔ x² + y² + 9 – 2xy - 6x + 6y + x² + y² + 1 + 2xy - 2x – 2y = 16

⇔ 2x² + 2y² - 8x + 4y – 6 = 0

⇔ x² + y² – 4x + 2y – 3 = 0

Đây là phương trình đường tròn tâm
I( 2; -1) và bán kính
r = = 2√2

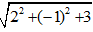
Chọn A

Ví dụ 5: Cho số phức z thỏa mãn là số thuần ảo. Tập hợp các điểm M biểu diễn số phức z là:

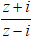
A. Đường tròn tâm O, bán kính R = 1.

B. Hình tròn tâm O, bán kính R = 1 (kể cả biên).

C. Hình tròn tâm O, bán kính R = 1 (không kể biên).

D. Đường tròn tâm O, bán kính R = 1 bỏ đi một điểm (0; 1).

Lời giải:

Gọi z = a + bi ; (a,b ∈ R) và điểm M(a, b) biểu diễn số phức z.

Ta có:

=

=
=

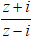
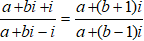
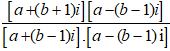
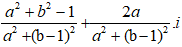
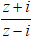
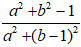
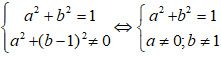
Để là số thuần ảo thì :

= 0
⇔

Do đó, tập hợp các điểm M là đường tròn tâm O, bán kính R = 1 và bỏ đi điểm
(0; 1).

Chọn D.

Dạng 4: Tập hợp điểm biểu diễn số phức là một miền

2. Ví dụ minh họa

Ví dụ 1: Cho số phức z= a + bi, (a,b ∈ R). Để điểm biểu diễn của z nằm trong dải (- 2; 2), ở hình 1, điều kiện của a và b là:

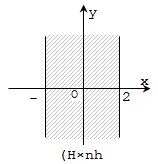
A. a,b ∈ (-2; 2) .    B. a ∈ (-2; 2); b ∈ R

C. a ∈ R; b ∈ (-2; 2)    D. a,b ∈ [-2; 2]

Lời giải:

Các số phức trong dải đã cho có phần thực trong khoảng (-2; 2), phần ảo tùy ý.

Do đó, a ∈ (-2; 2); b ∈ R

Chọn B.

Ví dụ 2: Số phức z thỏa mãn điều nào thì có điểm biểu diễn thuộc phần gạch chéo như trên hình.

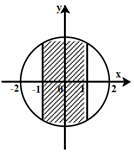
A. Số phức z = a + bi, |z| ≤ 2; a ∈ [-1; 1] .

B. Số phức z = a + bi, |z| ≤ 2; a ∉ [-1; 1] .

C. Số phức z = a + bi, |z| < 2; a ∈ (-1; 1) .

D. Số phức z = a + bi, |z| ≤ 2; b ∈ [-1; 1] .

Lời giải:

Từ hình biểu diễn ta thấy tập hợp các điểm M(a; b) biểu diễn số phức z trong phần gạch chéo đều thuộc đường tròn tâm O(0; 0) và bán kính bằng 2 ngoài ra -1 ≤ a ≤ 1 .

Vậy M(a, b) là điểm biểu diễn của các số phức z = a + bi có mô đun nhỏ hơn hoặc bằng 2 và có phần thực thuộc đoạn
[-1; 1].

Chọn A.

Ví dụ 3: Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ

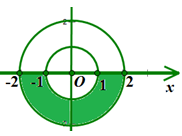
A. 1 ≤ |z| ≤ 2 và phần ảo dương.

B. 1 ≤ |z| ≤ 2 và phần ảo âm.

C. 1 < |z| < 2 và phần ảo dương.

D. 1 < |z| < 2 và phần ảo âm.

Lời giải:

Ta thấy phần tô màu là nửa dưới trục hoành của hình vành khăn được tạo bởi hai đường tròn đồng tâm O(0 ; 0) và bán kính lần lượt là 1 và 2

Vậy đây chính là tập hợp các điểm M(x, y) biểu diễn cho số phức z = x + yi trong mặt phẳng phức với 1 ≤ |z| ≤ 2 và có phần ảo âm.

Chọn B

Dạng 5: Tập hợp điểm biểu diễn số phức là đường elip

1. Phương pháp giải

+ Trong mặt phẳng, cho hai điểm cố định F₁, F₂, với F₁F₂ = 2c ( c > 0). Đường Elip là tập hợp các điểm M sao cho MF₁ + MF₂ = 2a trong đó a là số cho trước lớn hơn c.

Hai điểm F₁, F₂ được gọi là tiêu điểm của Elip. Khoảng cách 2c được gọi là tiêu cự của Elip.

+ Phương trình chính tắc của elíp có tiêu điểm F₁( - c; 0); F₂(c; 0)

= 1; (a > b > 0; b² = a² - c²)

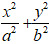
2. Ví dụ minh họa

Ví dụ 1: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z - 2| + |z + 2| = 6 trên mặt phẳng tọa độ là một

A. Đường thẳng.    B.Đường tròn.

C. Elip.    D. Hypebol.

Lời giải:

Trên mặt phẳng tọa độ Oxy, gọi M(x; y) biểu diễn số phức z = x + yi, .

Ta có |z - 2| + |z + 2| = 6

⇔ = 6 (1) .

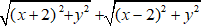
Đặt F₁(- 2; 0); F₂(2; 0);
khi đó (1) ⇔ MF₁ + MF₂ = 6

suy ra M nằm trên Elip có hai tiêu điểm là F₁, F₂ và bán kính trục lớn là a = 6/2 = 3

Suy ra: b² = a² – c² = 3² – 2² = 5

Phương trình của elip đó là: 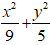= 1 .

Chọn C

Ví dụ 2: Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z - 3| + |z + 3| = 12.

A. Đường tròn (x – 3)² + (y + 3)² = 36 .

B. Elip 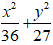= 1.

C. Đường tròn (x + 3)² + (y – 3)² = 144.

D. Elip 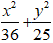= 1 .

Lời giải:

Gọi M(x, y) là điểm biểu diễn số phức
z = x + yi, (x,y ∈ R)

Gọi A( 3; 0); B( -3; 0).

Ta có: |z - 3| + |z + 3| = 12
⇔ MB + MA = 12.

Ta có AB = 6. Suy ra tập hợp điểm M biểu diễn số phức z là elip với 2 tiêu điểm là
A( 3; 0);

B(-3; 0), tiêu cự AB = 6 = 2c nên c = 3.

Độ dài trục lớn là 2a = 12 ⇒ a = 6

Khi đó, b² = a² – c² = 36 - 9 = 27.

Vậy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện
|z - 3| + |z + 3| = 12 là elip có phương trình:
= 1

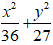
Chọn B.

Ví dụ 3: Cho số phức z thỏa mãn
|z - 4| + | z + 4| = 10. Giá trị lớn nhất và nhỏ nhất của môđun của số phức z là

A.10 và 4.    B. 5 và 4 .    C. 4 và 3 .    D. 5 và 3

Lời giải:

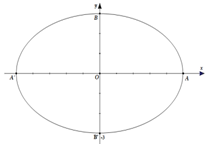
Giả sử z = x + yi,(x,y ∈ R) có điểm biểu diễn là M(x ; y).

Giả sử F₁ ( 4 ;0) ; F₂(- 4 ;0).

Ta có : | z- 4| + | z + 4| = 10
nên MF₁ + MF₂ =10

Khi đó tập hợp các điểm M thỏa mãn là đường elip (E) có các tiêu điểm là F₁ ; F₂ và trục lớn bằng 10.

Ta có 2c = F₁F₂ = 8 ⇔ c = 4 và 2a = 10
⇔ a = 5

suy ra b² = a² – c² = 25 – 16 = 9 ⇒ b= 3

Do đó, phương trình elip thỏa mãn là :
= 1

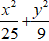
Vì M di động trên (E) nên |z|= OM lớn nhất, nhỏ nhất khi OM lần lượt là nửa độ dài trục lớn, nửa độ dài trục nhỏ.

⇒ max|z| = 5 ; min|z| = 3

Chọn D

Ví dụ 4: Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa đọ Oxy để
|2z - z−| ≤ 3 số phức z có phần thực không âm. Tính diện tích hình (H).

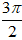
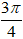
A. 3π    B.    C.    D. 6π

Lời giải:

Giả sử z = x + yi, (x,y ∈ R), khi đó z− = x - yi , giả thiết của bài toán là

|2z - z−| ≤ 3 ⇔ |2x + 2yi - (x - yi)| ≤ 3

⇔ |x + 3yi| ≤ 3 ⇔ x² + 9y² ≤ 9

⇔ ≤ 1

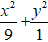
Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(x; y) thuộc miền trong của elip (E): ≤ 1 (kể cả các điểm trên biên).

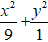
+ Bán trục lớn của (E) là a= 3, bán trục bé của (E) là b = 1 nên diện tích cần tính của miền (H) là

S = π.AB = 3π .

Chọn A.

Ví dụ 5: Cho số phức z thỏa mãn
+ = 4 . Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính M.n.

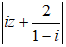
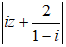
A. M.n = 2    B. M.n= 1

C. M.n = 2√2    D. M.n = 2√3.

Lời giải:

Ta có ; =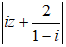
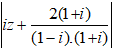
= |iz + 1 + i| = |-i(iz + 1 + i) = | z + 1 - i||

=
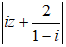
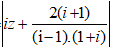
= |iz - 1 - i| = |-i.(iz - 1 - i) = |z - 1 + i||

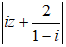
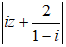
Theo giả thiết : + = 4 ⇔ | z + 1- i| + | z-1 + i| = 4 (*)

Đặt F₁( -1 ; 1); F₂( 1;-1) ⇒ F₁F₂ = 2√2 < 4

Gọi M là điểm biểu diễn số phức z. Khi đó, (*) trở thành: MF₁ + MF₂ = 4.

Suy ra quỹ tích điểm biểu diễn số phức z là elíp có tiêu điểm F₁, F₂ và độ dài trục lớn là 2a = 4 và tiêu cự 2c= F₁F₂ = 2√2 .

⇒ |z|=OM nên

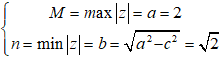
⇒ M.n = 2√2

Chọn C.