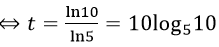7 Bài toán lãi suất, bài toán thực tế trong đề thi Đại học có lời giải - Toán lớp 12
7 Bài toán lãi suất, bài toán thực tế trong đề thi Đại học có lời giải
Với 7 Bài toán lãi suất, bài toán thực tế trong đề thi Đại học có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Bài toán lãi suất, bài toán thực tế từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1. Lãi đơn
1. Phương pháp giải
- Định nghĩa: số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra, tức là tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn kế tiếp, cho dù đến kì hạn người gửi không đến gửi tiền ra.
- Công thức tính: Khách hàng gửi vào ngân hàng A đồng với lãi đơn r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ N*) là:
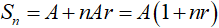
Chú ý: Trong tính toán các bài toán lãi suất và các bài toán liên quan, ta nhớ r% là 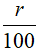
2. Ví dụ minh họa
Ví dụ 1. Chú Nam gửi vào ngân hàng 10 triệu đồng với lãi đơn 5%/năm thì sau 5 năm số tiền chú Nam nhận được cả vốn lẫn lãi là bao nhiêu?
A. 12,5 triệu B. 12 triệu C. 13 triệu D. 12, 8 triệu.
Lời giải:
Đáp án: A
Số tiền cả gốc lẫn lãi chú Nam nhận được sau 5 năm là:
S5 = 10.(1 + 5.0,05) = 12,5 (triệu đồng)
Ví dụ 2. Chị Hằng gửi ngân hàng 3 350 000 đồng, theo phương thức lãi đơn, với lãi suất 0,4 % trên nửa năm. Hỏi ít nhất bao lâu chị rút được cả vốn lẫn lãi là 4 020 000 đồng?
A. 5 năm. B. 30 tháng. C. 3 năm. D. 24 tháng.
Lời giải:
Đáp án: B
Gọi n là số chu kỳ gửi ngân hàng, áp dụng công thức lãi đơn ta có:
4 020 000 = 3 350 000 (1 + n.0,04)
Suy ra, n = 5 (chu kỳ) .
Mà nữa năm = 6 tháng
Vậy thời gian là 5 . 6= 30 tháng.
Ví dụ 3. Tính theo phương thức lãi đơn; để sau 2,5 năm rút được cả vốn lẫn lãi số tiền là 10 892 000 đồng với lãi suất 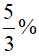
A. 9 336 000 B. 10 456 000. C.8 627 000. D. 9 215 000
Lời giải:
Đáp án: A
Đây là bài toán lãi đơn với chu kỳ là một quý = 3 tháng.
Vậy 2,5 năm = 30 tháng = 10 quý ( 10 chu kỳ).
Với x là số tiền gửi tiết kiệm, ta có:
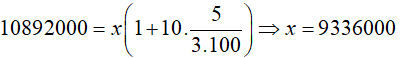
Ví dụ 4. Bạn Lan gửi 1500 USD với lãi suất đơn cố định theo quý. Sau 3 năm, số tiền bạn ấy nhận được cả gốc lẫn lãi là 2320 USD. Hỏi lãi suất tiết kiệm là bao nhiêu một quý? (làm tròn đến hàng phần nghìn)
A. 0,182. B. 0,046. C. 0, 015. D. 0, 037.
Lời giải:
Đáp án: B
Đây là bài toán lãi đơn, chu kỳ là một quý.
Ta có, 3 năm = 36 tháng = 12 quý
Áp dụng công thức, ta có: 2320 = 1500(1 + 12r%) , bấm máy tính ta được lãi suất là r% ≈ 0,046 một quý
Dạng 2. Lãi kép
1. Phương pháp giải
1. Định nghĩa
Lãi kép là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp.
2. Công thức tính
Khách hàng gửi vào ngân hàng A đồng với lãi kép r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ N*) là:
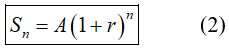
Chú ý: Từ công thức (2) ta có thể tính được:
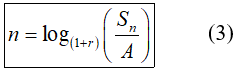
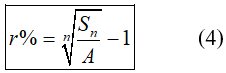
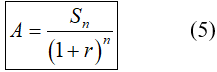
2. Ví dụ minh họa
Ví dụ 1. Chú Việt gửi vào ngân hàng 10 triệu đồng với lãi kép 5%/năm. Tính số tiền cả gốc lẫn lãi chú Việt nhận được sau khi gửi ngân hàng 10 năm (gần với số nào nhất)?
A. 16,234 triệu B. 16, 289 triệu C. 16, 327 triệu D.16, 280 triệu
Lời giải:
Đáp án: B
Số tiền cả gốc lẫn lãi nhận được sau 10 năm với lãi kép 5%/năm là
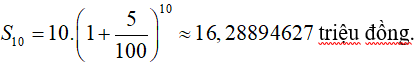
Ví dụ 2. Bạn An gửi tiết kiệm một số tiền ban đầu là 1000000 đồng với lãi suất 0,58%/tháng (không kỳ hạn). Hỏi bạn An phải gửi bao nhiêu tháng thì được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng ?
A. 46 tháng B. 44 tháng C. 45 tháng D. 47 tháng
Lời giải:
Đáp án: A
Áp dụng công thức ( 3) ta có số kì hạn là:
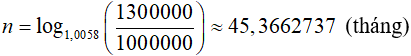
Nên để nhận được số tiền cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng thì bạn An phải gửi ít nhất là 46 tháng.
Ví dụ 3. Lãi suất của tiền gửi tiết kiệm của một số ngân hàng thời gian vừa qua liên tục thay đổi. Bạn Châu gửi số tiền ban đầu là 5 triệu đồng với lãi suất 0,7% tháng chưa đầy một năm, thì lãi suất tăng lên 1,15% tháng trong nửa năm tiếp theo và bạn Châu tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 0,9% tháng, bạn Châu tiếp tục gửi thêm một số tháng tròn nữa, khi rút tiền bạn Châu được cả vốn lẫn lãi là 5 747 478,359 đồng (chưa làm tròn). Hỏi bạn Châu đã gửi tiền tiết kiệm trong bao nhiêu tháng?
A. 10 tháng B. 12 tháng C. 14 tháng D.15 tháng
Lời giải:
Đáp án: D
Gọi X; Y (X, Y ∈ Z+: X, Y ≤ 12) lần lượt là số tháng bạn Châu đã gửi với lãi suất 0,7%/tháng và 0,9%/tháng . Theo công thức lãi kép, ta có số tiền bạn Châu thu được cuối cùng là:
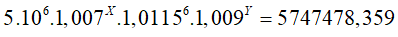
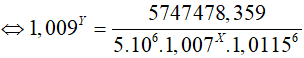
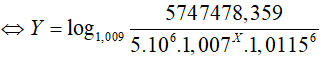
Kết hợp điều kiện; X và Y nguyên dương ta thấy X= 5 và Y= 4 thỏa mãn.
(Nhập vào máy tính 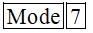
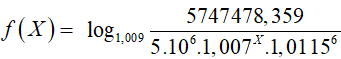
Vậy bạn Châu đã gửi tiền tiết kiệm trong: 5+6+ 4= 15 tháng.
Ví dụ 4. Chị Thanh gửi ngân hàng 155 triệu đồng, với lãi suất 1,02 % một quý. Hỏi sau một năm số tiền lãi chị nhận được là bao nhiêu? (làm tròn đến hàng nghìn)
A. 161 421 000. B. 161 324 000 C. 7 698 000 D. 6 421 000
Lời giải:
Đáp án: D
Số tiền lãi chính là tổng số tiền cả gốc lẫn lãi trừ đi số tiền gốc.
Áp dụng công thức lãi kép với 12 tháng= 4 quý (n = 4) nên số tiền lãi là 155. (1 + 0,0102)4 − 155 ≈ 6421000 (đồng).
Ví dụ 5. Một khách hàng gửi tiết kiệm 64 triệu đồng, với lãi suất 0,85% một tháng. Hỏi người đó phải mất ít nhất mấy tháng để được số tiền cả gốc lẫn lãi không dưới 72 triệu đồng?
A.13 B. 14 C. 15 D 16
Lời giải:
Đáp án: B
Gọi n là số tháng cần tìm, áp dụng công thức lãi kép ta có n là số tự nhiên nhỏ nhất thỏa mãn :
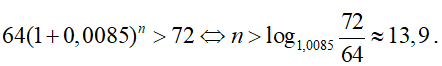
Ví dụ 6. Một khách hàng gửi ngân hàng 20 triệu đồng, kỳ hạn 3 tháng, với lãi suất 0,65 % một tháng theo phương thức lãi kép. Hỏi sau bao lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.
A. 8 năm 11 tháng. B. 19 tháng. C. 18 tháng. D. 9 năm.
Lời giải:
Đáp án: D
Lãi suất theo kỳ hạn 3 tháng là 3. 0,65 % = 1,95 %
Gọi n là số kỳ hạn cần tìm. Theo giả thiết ta có n là số tự nhiên nhỏ nhất thỏa mãn:
20. (1+ 0,0195)n − 20 > 20
Ta được n = 36 chu kỳ, một chu kỳ là 3 tháng.
Nên thời gian cần tìm là 36. 3= 108 tháng = 9 năm.
Dạng 3. Tiền gửi hàng tháng
1. Phương pháp giải
- Định nghĩa
Mỗi tháng gửi đúng cùng một số tiền vào 1 thời gian cố định.
- Công thức tính
Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng, với lãi kép r%/tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng ( n ∈ N* ) ( nhận tiền cuối tháng, khi ngân hàng đã tính lãi) là Sn.
Ý tưởng hình thành công thức:
+ Cuối tháng thứ nhất, khi ngân hàng đã tính lãi thì số tiền có được là
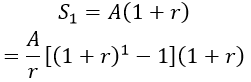
+ Đầu tháng thứ hai, khi đã gửi thêm số tiền đồng thì số tiền là
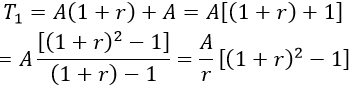
+ Cuối tháng thứ hai, khi ngân hàng đã tính lãi thì số tiền có được là
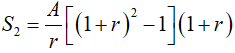
+ Từ đó ta có công thức tổng quát
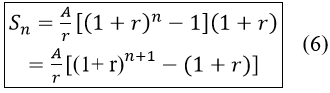
Chú ý: Từ công thức (6) ta có thể tính được:
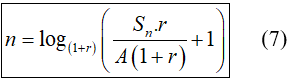
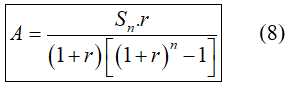
2. Ví dụ minh họa
Ví dụ 1. Đầu mỗi tháng ông Mạnh gửi ngân hàng 580 000 đồng với lãi suất 0,7%/tháng. Sau 10 tháng thì số tiền ông Mạnh nhận được cả gốc lẫn lãi (sau khi ngân hàng đã tính lãi tháng cuối cùng) là bao nhiêu?
A. 6 028 056 đồng B. 6 002 765 đồng
C. 6 012 654 đồng D. 6 001 982 đồng
Lời giải:
Đáp án: A
Áp dụng công thức (6), số tiền ông Mạnh nhận được cả gốc lẫn lãi là:
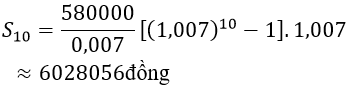
Ví dụ 2. Ông Nghĩa muốn có ít nhất 100 triệu đồng sau 10 tháng kể từ khi gửi ngân hàng với lãi 0,7%/tháng thì mỗi tháng ông Nghĩa phải gửi số tiền ít nhất bao nhiêu?
A. 9,623 triệu B. 9,622 triệu C. 9,723 triệu D. 9,564 triệu
Lời giải:
Đáp án: B
Áp dụng công thức ( 8), số tiền mà ông Nghĩa cần gửi mỗi tháng là:
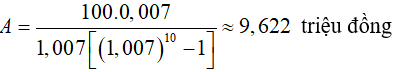
Ví dụ 3. Đầu mỗi tháng anh Thắng gửi vào ngân hàng số tiền 3 triệu đồng với lãi suất 0,6%/tháng. Hỏi sau ít nhất bao nhiêu tháng ( khi ngân hàng đã tính lãi) thì anh Thắng được số tiền cả gốc lẫn lãi từ 100 triệu trở lên?
A. 28 tháng B. 29 tháng C. 30 tháng D . 31 tháng.
Lời giải:
Đáp án: D
Áp dụng công thức (7), số tháng ít nhất anh Thắng phải gửi để được số tiền cả gốc lẫn lãi từ 100 triệu trở lên là:
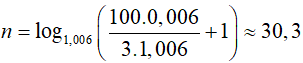
Vậy anh Thắng phải gửi ít nhất là 31 tháng mới được số tiền cả gốc lẫn lãi từ 100 triệu trở lên.
Ví dụ 4. Bạn muốn có 3000 USD để đi du lịch châu Âu. Để sau 4 năm thực hiện được ý định thì hàng tháng bạn phải gửi tiết kiệm bao nhiêu (làm tròn đến hàng đơn vị)? Biết lãi suất 0,83 % một tháng.
A. 62 USD. B.61 USD. D. 51 USD . D. 42 USD.
Lời giải:
Đáp án: D
Gọi X (USD) là số tiền hàng tháng gửi tiết kiệm.
Ta có 4 năm = 12.4 = 48 tháng.
Áp dụng công thức ( 6) ta có:
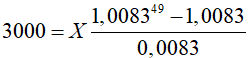
bấm máy tính ta được X ≈ 50,7 (USD). Do đó, mỗi tháng phải gửi 51 USD.
Ví dụ 5. Anh A gửi tiết kiệm hàng tháng với số tiền 20 000 000 đồng vào ngân hàng với lãi suất 0,7% một tháng dự định gửi trong vào 36 tháng. Nhưng đến đầu tháng thứ 25 thì anh A làm ăn thua lô không còn tiền để gửi vào ngân hàng nên buộc phải rút tiền ra khỏi ngân hàng đó. Biết số tiền thua lô là 500 000 000 đồng. Hỏi sau khi rút tiền ra ngân hàng thì số tiền rút được T bằng bao nhiêu ? Anh A còn nợ hay đã trả hết rồi ?
A. vẫn còn nợ , T= 424 343 391 đồng. B. Đã trả hết, T= 548 153 795 đồng.
C. Đã trả hết , T= 524 343 391 đồng. D. vẫn còn nợ , T= 448 153 795 đồng.
Lời giải:
Đáp án: C
Chú ý:” đến đầu tháng thứ 25 thì anh A làm ăn thua lô không còn tiền để gửi vào ngân hàng nên buộc phải rút tiền ra khỏi ngân hàng đó”. Như vậy, anh A đã gửi đều đặn được 24 tháng.
Dạng toán gửi đều đặn hàng tháng
Số tiền anh nhận được:
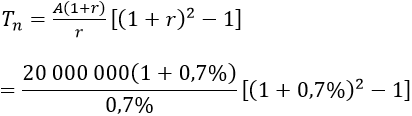
= 524343391 đồng
Dạng 4. Gửi ngân hàng và rút tiền gửi hàng tháng
1. Phương pháp giải
- Định nghĩa
Gửi ngân hàng số tiền là A đồng với lãi suất r%/tháng. Mỗi tháng vào ngày ngân hàng tính lãi, rút ra số tiền là X đồng. Tính số tiền còn lại sau n tháng là bao nhiêu?
- Công thức tính
Ý tưởng hình thành công thức:
+ Cuối tháng thứ nhất, khi ngân hàng đã tính lãi thì số tiền có được là T1 = A(1 + r) và sau khi rút số tiền còn lại là
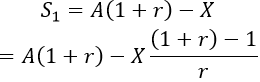
+ Cuối tháng thứ hai, khi ngân hàng đã tính lãi thì số tiền có được là
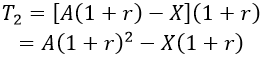
và sau khi rút số tiền còn lại là
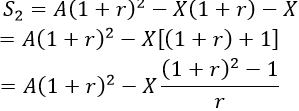
+ Từ đó ta có công thức tổng quát số tiền còn lại sau tháng là
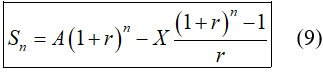
Chú ý: Từ công thức (9) ta có thể tính được:
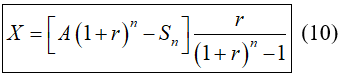
2. Ví dụ minh họa
Ví dụ 1. Anh Chiến gửi ngân hàng 20 triệu đồng với lãi suất 0,75%/tháng. Mỗi tháng vào ngày ngân hàng tính lãi, anh Chiến đến ngân hàng rút 300 nghìn đồng để chi tiêu. Hỏi sau 2 năm số tiền anh Chiến còn lại trong ngân hàng là bao nhiêu?
A.16 071 729 đồng B. 16 189 982 đồng
C. 17 012 123 đồng D. 17 872 134 đồng
Lời giải:
Đáp án: A
Áp dụng công thức (9) , ta có số tiền anh Chiến còn lại trong ngân hàng sau 2 năm là:
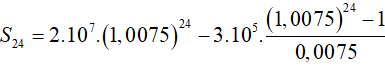
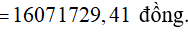
Ví dụ 2. Anh Chiến gửi ngân hàng 20 triệu đồng với lãi suất 0,7%/tháng. Mỗi tháng vào ngày ngân hàng tính lãi, anh Chiến rút một số tiền như nhau để chi tiêu. Hỏi số tiền ( gần nhất) mỗi tháng anh Chiến rút là bao nhiêu để sau 5 năm thì số tiền vừa hết?
A. 409 219 đồng B. 409 367 đồng C. 423 356 đồng D. 432 123 đồng
Lời giải:
Đáp án: B
Áp dụng công thức (10)
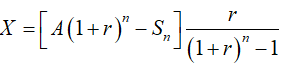
Trong đó, A = 20 triệu đồng; r= 0,7%/ tháng, n = 5. 12 = 60 tháng và Sn = 0 ( vì khi đó anh Chiến đã rút hết tiền) ta được:
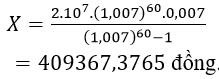
Ví dụ 3. Chú Tư gửi vào ngân hàng 50 triệu đồng với lãi suất 0,6%/tháng. Sau mỗi tháng, chú Tư đến ngân hàng rút mỗi tháng 3 triệu đồng để chi tiêu cho đến khi hết tiền thì thôi. Sau một số tròn tháng thì chú Tư rút hết tiền cả gốc lẫn lãi. Biết trong suốt thời gian đó, ngoài số tiền rút mỗi tháng chú Tư không rút thêm một đồng nào kể cả gốc lẫn lãi và lãi suất không đổi. Vậy tháng cuối cùng chú Tư sẽ rút được số tiền là bao nhiêu (làm tròn đến đồng)?
A. 1840270 đồng. B.3 000 000 đồng.
C. 1840269 đồng. D. 1840271 đồng.
Lời giải:
Đáp án: A
Áp dụng công thức tính số tiền còn lại sau n tháng
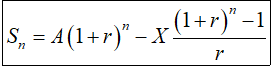
Với A= 50 triệu đồng, r = 0, 6 và X= 3 triệu đồng ta được:
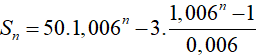 .
.
Để rút hết số tiền thì ta tìm số nguyên dương n nhỏ nhất sao cho:
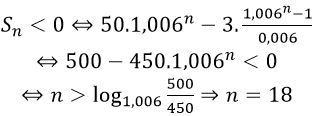
Khi đó số tiền tháng cuối cùng mà chú Tư rút là
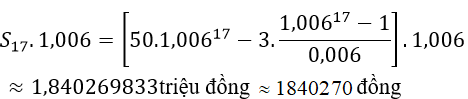
Ví dụ 4. Bà B gửi vào ngân hàng 100 triệu đồng với lãi suất 6%/năm, kì hạn 1 tháng. Môi tháng bà B vào ngân hàng rút 5 triệu để mua sắm. Hỏi sau bao nhiêu tháng bà B rút hết cả vốn lẫn lãi từ ngân hàng ? Biết lãi suất được tính đều đặn
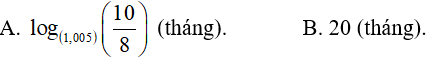
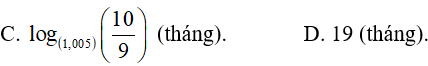
Lời giải:
Đáp án: C
Ta có công thức:
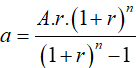
Gọi n thời gian rút hết tiền trong số tiết kiệm:
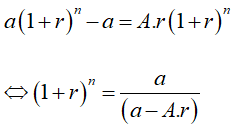
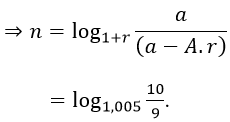
Dạng 5. Vay vốn trả góp
1. Phương pháp giải
1. Định nghĩa.
Vay ngân hàng số tiền là A đồng với lãi suất r%/tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ cách nhau đúng một tháng, mỗi hoàn nợ số tiền là X đồng và trả hết tiền nợ sau đúng n tháng.
2.Công thức tính
Cách tính số tiền còn lại sau n tháng giống hoàn toàn công thức tính gửi ngân hàng và rút tiền hàng tháng nên ta có
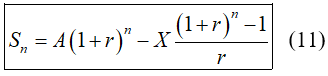
Để sau đúng n tháng trả hết nợ thì Sn = 0 nên
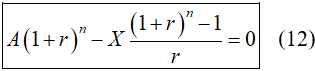
và
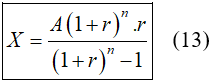
2. Ví dụ minh họa
Ví dụ 1. Chị Ngọc vay trả góp ngân hàng số tiền 50 triệu đồng với lãi suất 1,15%/tháng trong vòng 4 năm thì mỗi tháng chị Ngọc phải trả gần với số tiền nào nhất ?
A. 1 362 000 đồng B. 1 432 000 đồng
C. 1 361 000 đồng D. 1 232 000 đồng
Lời giải:
Đáp án: C
Áp dụng công thức (13) với A = 50 triệu; r= 1,15 % và n= 4.12= 48 tháng. Số tiền chị Ngọc phải trả mỗi tháng là:
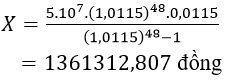
Ví dụ 2. Anh Sơn vay trả góp ngân hàng số tiền 500 triệu đồng với lãi suất 0,9%/tháng , mỗi tháng trả 15 triệu đồng. Sau bao nhiêu tháng thì anh Sơn trả hết nợ?
A. 40 tháng B. 36 tháng
C.38 tháng D. 39 tháng
Lời giải:
Đáp án: A
Áp dụng công thức 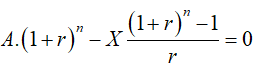
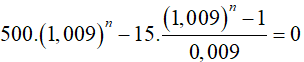
giải được n = 39, 80862049 ( tháng)
Do đó, để trả hết nợ thì anh Sơn phải trả nợ trong vòng 40 tháng.
Ví dụ 3. Một người vay ngân hàng số tiền 350 triệu đồng, mỗi tháng trả góp 8 triệu đồng và lãi suất cho số tiền chưa trả là 0,79% một tháng. Kỳ trả đầu tiên là cuối tháng thứ nhất. Hỏi số tiền phải trả ở kỳ cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn)
A. 2 921 000. B. 7 084 000
C. 2 944 000. D. 7 140 000
Lời giải:
Đáp án: D
Kỳ trả đầu tiên là cuối tháng thứ nhất nên đây là bài toán vay vốn trả góp cuối kỳ.
Gọi A là số tiền vay ngân hàng, B là số tiền trả trong mỗi chu kỳ, d= r% là lãi suất cho số tiền chưa trả trên một chu kỳ, n là số kỳ trả nợ.
Số tiền còn nợ ngân hàng (tính cả lãi) trong từng chu kỳ như sau:
+ Đầu kỳ thứ nhất là A.
+ Cuối kỳ thứ nhất là A(1+ d) − B.
+ Cuối kỳ thứ hai là :
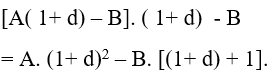
+ Cuối kỳ thứ ba là :
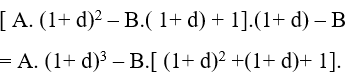
……
+ Theo giả thiết quy nạp, cuối kỳ thứ n là
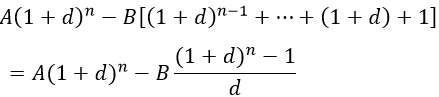
Vậy số tiền còn nợ (tính cả lãi) sau n chu kỳ là
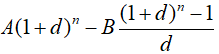
Trở lại bài toán, gọi n (tháng) là số kỳ trả hết nợ.
Khi đó, ta có:
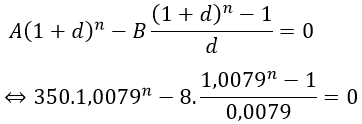
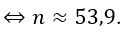
Tức là phải mất 54 tháng người này mới trả hết nợ.
Cuối tháng thư 53, số tiền còn nợ (tính cả lãi) là :
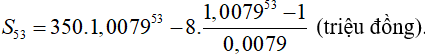
Kỳ trả nợ tiếp theo là cuối tháng thứ 54 , khi đó phải trả số tiền S53 và lãi của số tiền này nữa là :
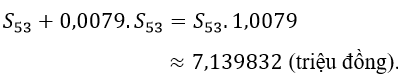
Ví dụ 4. Anh Bình vay ngân hàng 2 tỷ đồng để xây nhà và trả dần mỗi năm 500 triệu đồng. Kỳ trả đầu tiên là sau khi nhận vốn với lãi suất trả chậm 9% một năm. Hỏi sau mấy năm anh Bình mới trả hết nợ đã vay?
A. 6 B. 3 C. 4 D. 5
Lời giải:
Đáp án: D
Kỳ trả nợ đầu tiên là sau khi nhận vốn nên đây là bài toán vay vốn trả góp đầu kỳ.
Gọi A là số tiền vay ngân hàng, B là số tiền trả trong mỗi chu kỳ, d= r% là lãi suất trả chậm (tức là lãi suất cho số tiền còn nợ ngân hàng) trên một chu kỳ, n là số kỳ trả nợ.
Số tiền còn nợ ngân hàng (tính cả lãi) trong từng chu kỳ như sau:
+ Đầu kỳ thứ nhất là A − B.
+ Đầu kỳ thứ hai là
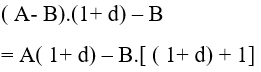
+ Đầu kỳ thứ ba là :
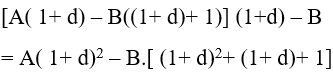
……
+ Theo giả thiết quy nạp, đầu kỳ thứ n là
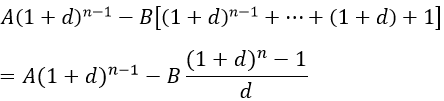
Vậy số tiền còn nợ (tính cả lãi) sau n chu kỳ là
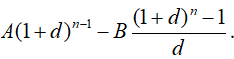
Trở lại bài toán, để sau n năm (chu kỳ ở đây ứng với một năm) anh Bình trả hết nợ thì ta có
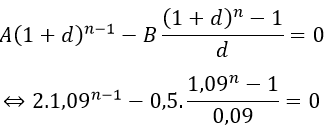
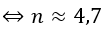
Vậy phải sau 5 năm anh Bình mới trả hết nợ đã vay.
Ví dụ 5. Ông A mua được căn nhà ở uận 1 với giá 2 tỷ đồng. với số tiền quá lớn buộc ông A phải trả góp với lãi suất hàng tháng là 0,5%. Hàng tháng ông trả 30 triệu đồng (bắt đầu từ khi mua nhà). Hỏi sau 36 tháng thì số tiền ông còn nợ là (làm tròn đến đơn vị triệu):
A. 1209 triệu đồng. B. 1207 triệu đồng.
C.1205 triệu đồng. D. 1200 triệu đồng.
Lời giải:
Đáp án: B
* Số tiền còn lại sau 36 tháng được tính theo công thức:
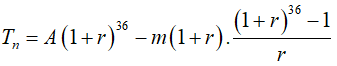
* Với A là số tiền nợ ban đầu , m là số tiền trả hàng tháng , r là lãi suất.
Ta có:
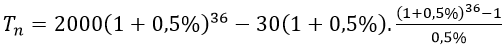

Dạng 6. Lãi kép liên tục
1. Phương pháp giải
* Gửi vào ngân hàng A đồng với lãi kép r%/năm thì số tiền nhận được cả vốn lẫn lãi sau n năm là: Sn = A. (1 + r)n
* Giả sử ta chia mỗi năm thành m kì hạn để tính lãi và lãi suất mỗi kì hạn là 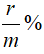
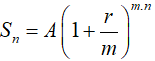
Khi tăng số kì hạn của mỗi năm lên vô cực, tức là , gọi là hình thức lãi kép tiên tục thì người ta chứng minh được số tiền nhận được cả gốc lẫn lãi là:
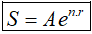
Công thức trên còn gọi là công thức tăng trưởng mũ.
2. Ví dụ minh họa
Ví dụ 1. Biết rằng đầu năm 2010, dân số Việt Nam là 86932500 người và tỉ lệ tăng dân số năm đó là 1,7% và sự tăng dân số được tính theo công thức tăng trưởng mũ. Hỏi cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 100 triệu người?
A. 2016 B. 2017
C. 2018 D. 2019
Lời giải:
Đáp án: C
Áp dụng công thức tăng trưởng mũ, ta có
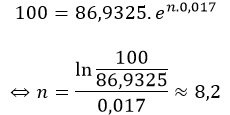
Vậy cứ tăng dân số với tỉ lệ như vậy thì đến năm 2018 dân số nước ta ở mức 100 triệu người.
Ví dụ 2. Tỉ lệ tăng dân số hàng năm của In-đô-nê-xi-a là 1,5%. Năm 1998, dân số của nước này là 212 942 000 người. Hỏi dần số của In-đô-nê-xi-a vào năm 2006 gần với số nào sau đây nhất?
A. 240091000 B.250091000.
C.230091000 D.220091000
Lời giải:
Đáp án: A
Áp dụng công thức tăng trưởng dân số Pn = P0.en.r
Với n= 2006 − 1998 = 8; r = 1,5 % và Po = 212942000
Ta có
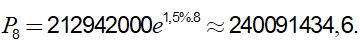
Ví dụ 3. Biết rằng tỉ lệ giảm dân hàng năm của Nga là 0, 5%. Năm 1998, dân số của Nga là 146861000 người. Hỏi năm 2008 dân số của Nga gần với số nào sau đây nhất?
A. 135699000. B.139699000.
C.140699000. D.145699000
Lời giải:
Đáp án: A
Áp dụng công thức tăng trưởng dân số: Pn = P0.en.r
Với n = 2008 − 1998 = 10; r = − 0,5% và P0 = 146861000
Ta có
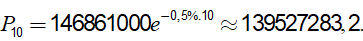
Ví dụ 4. Áp suất không khí P (đo bằng milimet thuỷ ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao x ( đo bằng mét), tức P giảm theo công thức P = P0.ex.i trong đó Po = 760 mmHg là áp suất ở mực nước biển ( x = 0 ), i là hệ số suy giảm. Biết rằng ở độ cao 1000 m thì áp suất của không khí là 672, 71 mmHg. Hỏi áp suất không khí ở độ cao 3000 m gần với số nào sau đây nhất?
A. 530, 23 mmHg. B. 540, 23 mmHg.
C. 520,23 mmHg. D. 510, 23 mmHg.
Lời giải:
Đáp án: A
Áp dụng công thức P = P0. ex.i với P0 = 760; x = 1000 thì P = 672, 71
Ta tìm được hệ số suy giảm
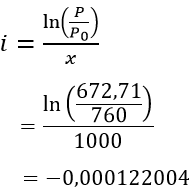
Vậy với x = 3000 thì
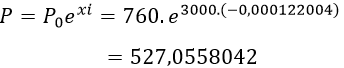
Gần với đáp án A nhất.
Ví dụ 5. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức f(t) = A. er.t, trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng ( r > 0 ), t (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
A. 5ln 20 (giờ). B. 5 (giờ).
C. 10log510 (giờ). D. 10log5 20 (giờ).
Lời giải:
Đáp án: C
Số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con.
Áp dụng công thức f(t) = A. er.t, ta có
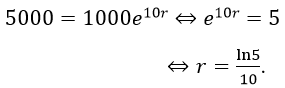
Gọi t là thời gian cần tìm để số lượng vi khuẩn tăng gấp 10 lần.
Do đó: