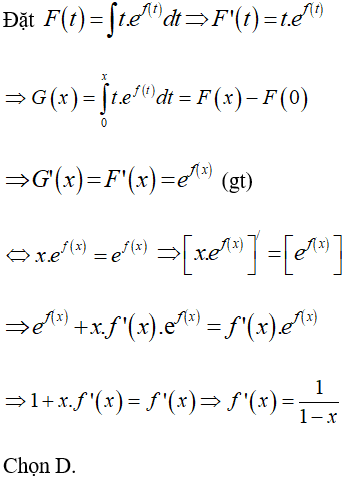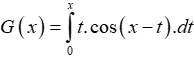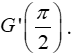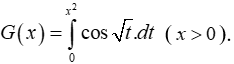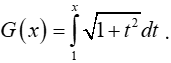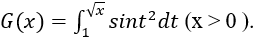30 Bài tập tích phân nâng cao chọn lọc, có lời giải - Toán lớp 12

---

30 Bài tập tích phân nâng cao chọn lọc, có lời giải

Với 30 Bài tập tích phân nâng cao chọn lọc, có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tích phân nâng cao từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Ví dụ minh họa

Ví dụ 1. Cho hàm số y = f(x) liên tục và có đạo hàm cấp hai trên [0;1] thỏa mãn:

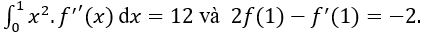
Tính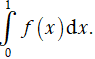

A. 10     B. 14.     C. 8.     D. 5.

Lời giải

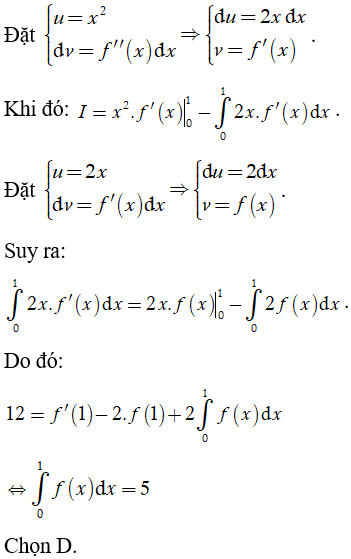
Ví dụ 2. Cho hàm số y = f(x) thỏa mãn:

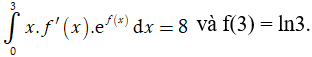
Tính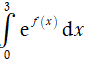

A. 1.     B. 11.     C. 8 - ln3.     D. 8 + ln3.

Lời giải

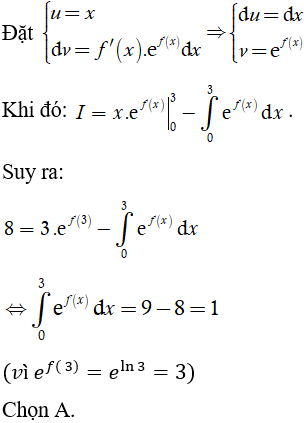
Ví dụ 3. Cho hàm số y = f(x) thỏa mãn:

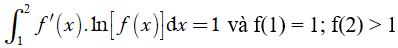
Giá trị của f(2) bằng:

A. f(2) = 2.     B. f(2) = 3.     C. f(2) = e.     D. f(2) = e².

Lời giải

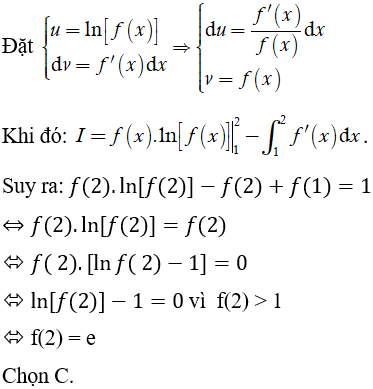
Ví dụ 4. Cho hàm số y = f(x) có đạo hàm và liên tục trên [0;2] thỏa mãn:

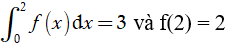
Tính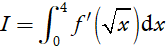

A. I = 2.     B. I = 3.     C. I = 5.     D. I = 1.

Lời giải

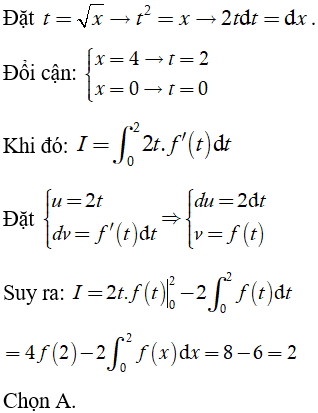
Ví dụ 5. Cho hàm số y = f(x) có đạo hàm và liên tục trên [0;1] và thỏa mãn:

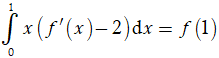
Giá trị của 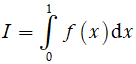bằng:

A. 1.     B. 2.     C. -1.     D. -2.

Lời giải

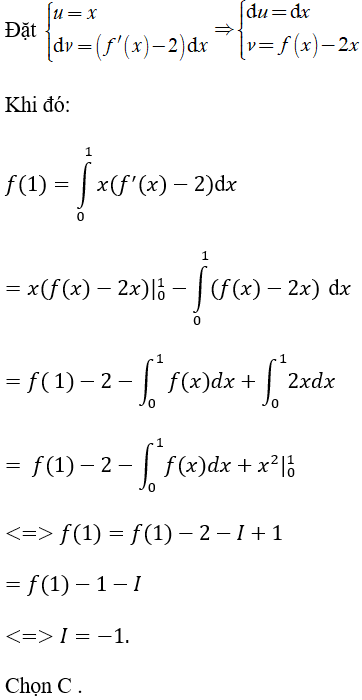
Ví dụ 6. Cho hàm số y = f(x) có đạo hàm và liên tục trên [0;1] và thỏa mãn:

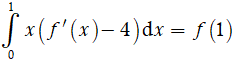
Giá trị của 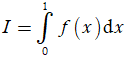bằng:

A. 0.     B. -2.     C. -1.     D. 2.

Lời giải

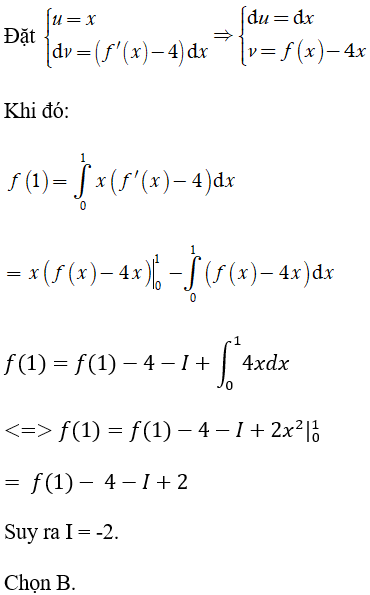
Ví dụ 7. Cho hàm số y = f(x) liên tục trên R thỏa mãn:

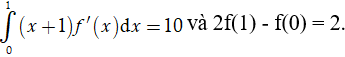
Tính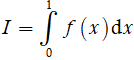

A. I = -12.     B. I = 8.     C. I = 12.     D. I = -8.

Lời giải

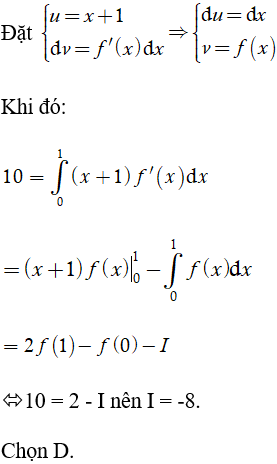
Ví dụ 8. Cho hàm số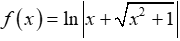

Tính tích phân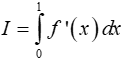

A. I = ln√2.     B. I = ln(1 + √2).     C. I = ln2.     D. I = 2ln2.

Lời giải

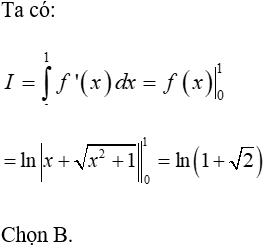
Ví dụ 9. Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [1;ln3] và thỏa mãn:

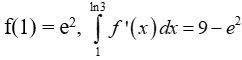
Tính I = f(ln3)?

A. I = 9 – 2e².     B. I = 9.     C. I = -9.     D. I = 2e² - 9.

Lời giải

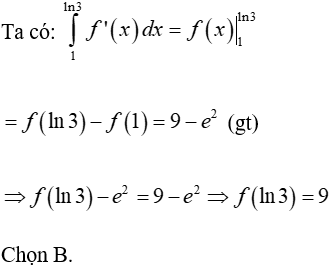
Ví dụ 10. Cho hai hàm số y = f(x) và y = g(x) có đạo hàm liên tục trên đoạn [0;1] và thỏa mãn:

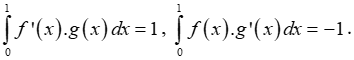
Tính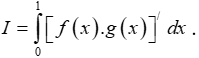

A. I = -2.     B. I = 0.     C. I = 3.     D. I = 2T.

Lời giải

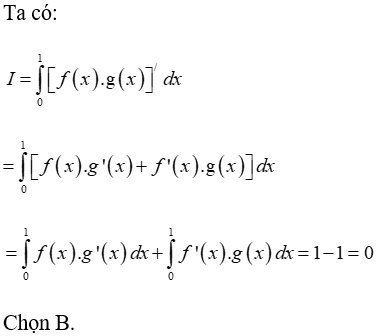
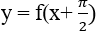
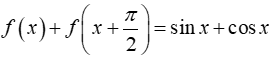
Ví dụ 11. Biết hàm số là hàm số chẵn trên đoạn [-π/2;π/2] và

Tính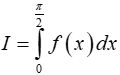

A. I = 0.     B. I = 1.     C. I = 2.     D. I = -1.

Lời giải

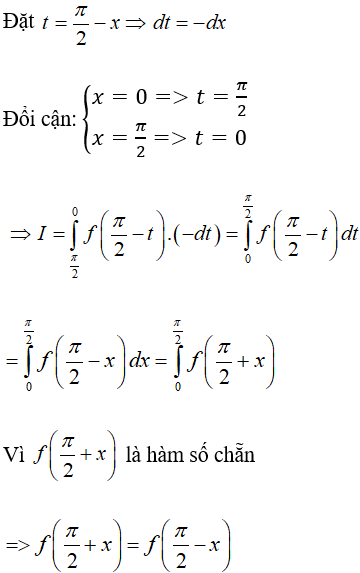
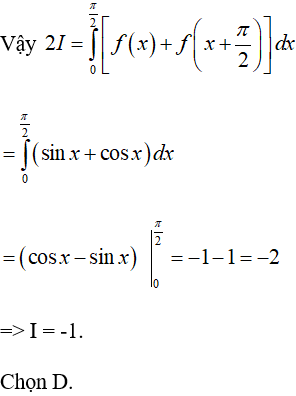
Ví dụ 12. Cho hàm số y = f(x) liên tục trên R, thỏa mãn f(-x) + 2018f(x) = e^x. Tính:

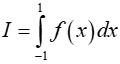
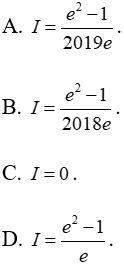
Lời giải

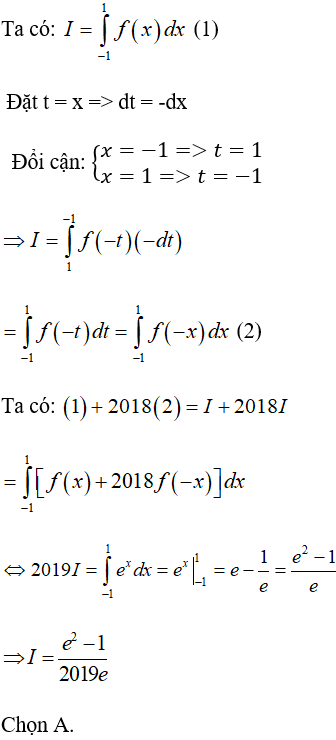
Ví dụ 13. Cho hàm số y = f(x) thỏa mãn:

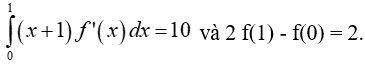
Tính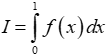

A. I = 8.     B. I = -8.     C. I = 4.     D. I = -4.

Lời giải

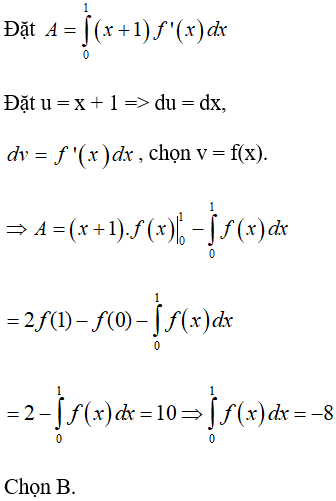
B. Bài tập vận dụng

Câu 1: Biết rằng hàm số y = f(x) liên tục trên R thỏa mãn:

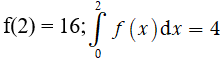
Tính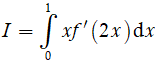

A. I = 3.     B. I = 12.     C. I = 20.     D. I = 7.

Lời giải:

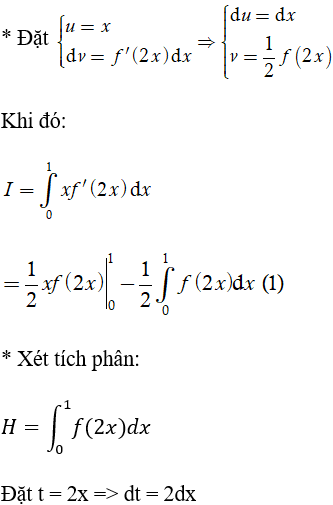
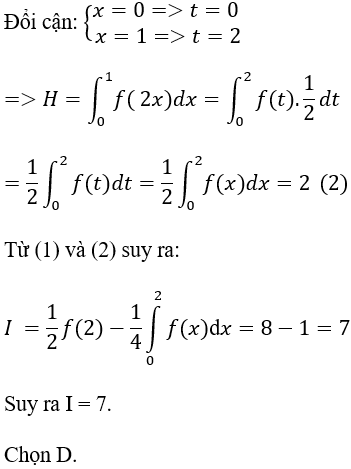
Câu 2: Cho hàm số y = f(x) có đạo hàm là f'(x) liên tục trên đoạn [0;1] và f(1) = 2.

Biết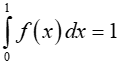

Tính tích phân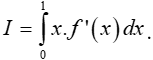

A. I = 1.     B. I = -1.     C. I = 3.     D. I = -3.

Lời giải:

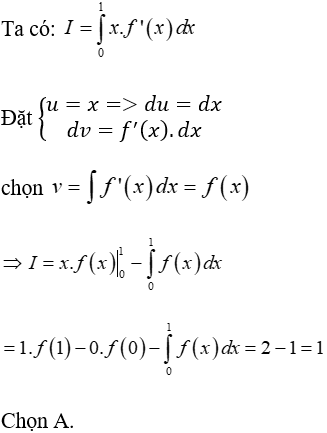
Câu 3: Cho hàm số y = f(x) có đạo hàm là f'(x) liên tục trên đoạn [0;1] và f(1) = 2.

Biết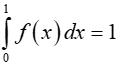

Tính tích phân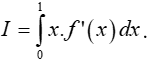

A. I = 1.     B. I = -1.     C. I = 3.     D. I = -3.

Lời giải:

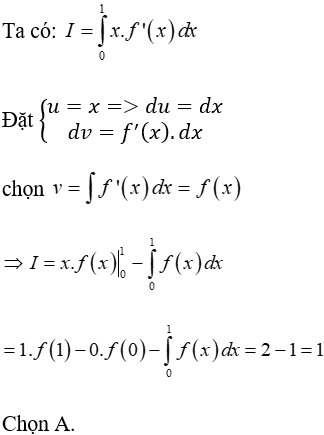
Câu 4: Cho hàm số y = f(x) thỏa mãn f(0) = f(1) = 1.

Biết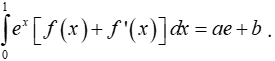

Tính biểu thức Q = a²⁰¹⁸ + b²⁰¹⁸.

A. Q = 8.     B. Q = 6.     C. Q = 4.     D. Q = 2.

Lời giải:

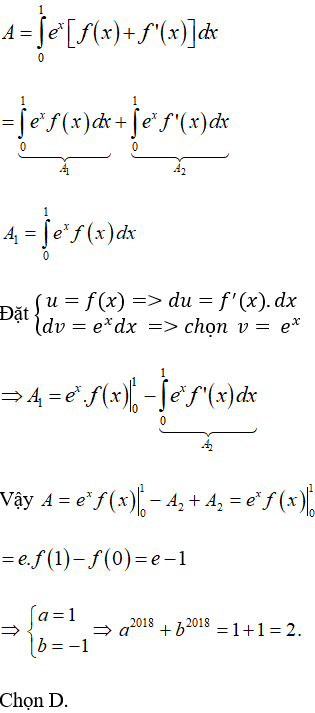
Câu 5: Cho hàm số y = f(x) liên tục trên

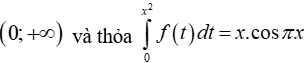
Tính f(4).

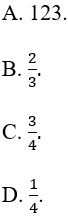
Lời giải:

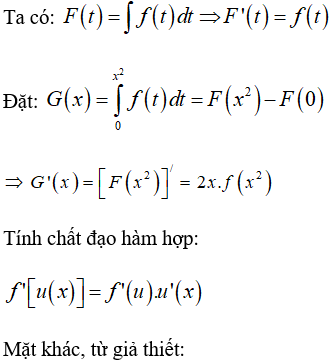
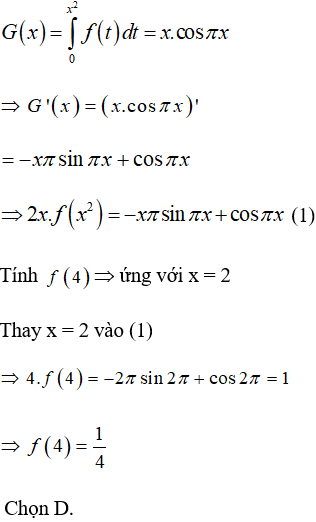
Câu 6: Cho hàm số y = f(x) thỏa mãn:

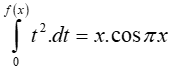
Tính f(4).

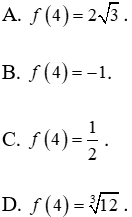
Lời giải:

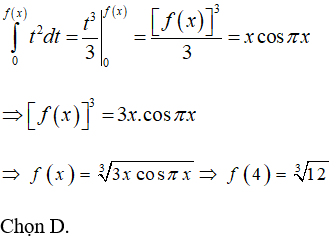
Câu 7: Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [1,2] và thỏa mãn f(x) > 0 khi x ∈ [1,2].

Biết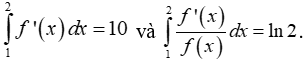

Tính f(2).

A. -10.     B. 20.     C. 10.     D. -20.

Lời giải:

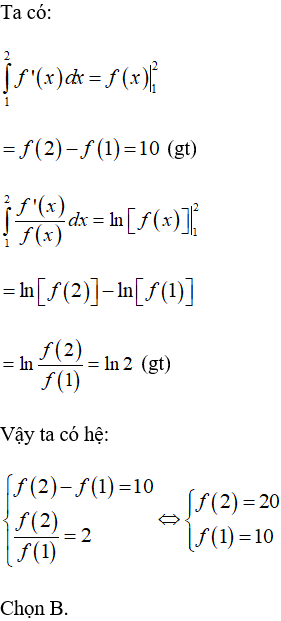
Câu 8: Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [-1,1], thỏa mãn f(x) > 0 với mọi x ∈ R và f'(x) + 2f(x) = 0. Biết f(1) = 1, tính f(-1).

A. e^-2.     B. e³.     C. e⁴.     D. 3.

Lời giải:

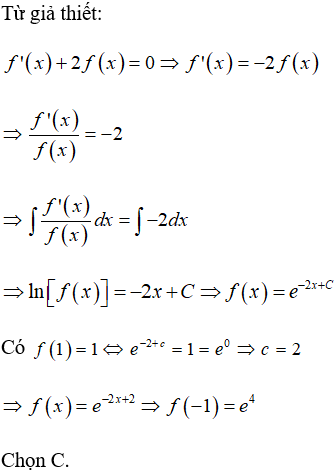
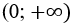
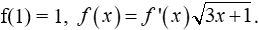
Câu 9: Cho hàm số y = f(x) có đạo hàm liên tục trên R, nhận giá trị dương trên khoảng và thỏa mãn

Mệnh đề nào đúng?

A. 1 < f(5) < 2.     B. 4 < f (5) < 5.     C. 2 < f(5) < 3.     D. 3 < f(5) < 4.

Lời giải:

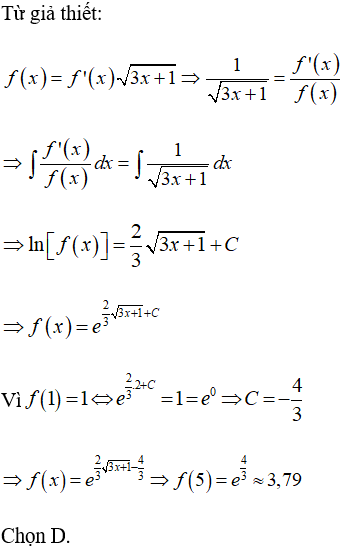
Câu 10: Cho hàm số y = f(x) có đạo hàm liên tục trên R và f(x) > 0 khi x ∈ [0;a] (a > 0).

Biết f(x).f(a - x) = 1, tính tích phân:

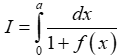
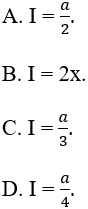
Lời giải:

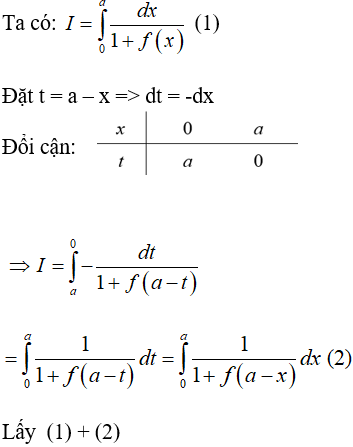
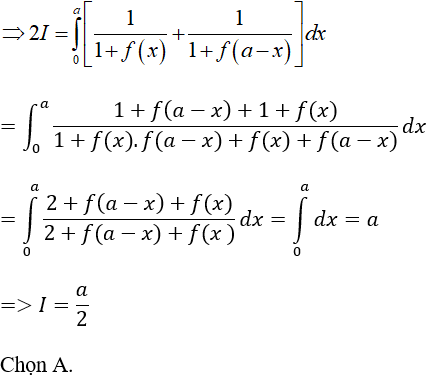
Câu 11: Cho hàm số

Tính

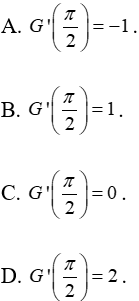
Lời giải:

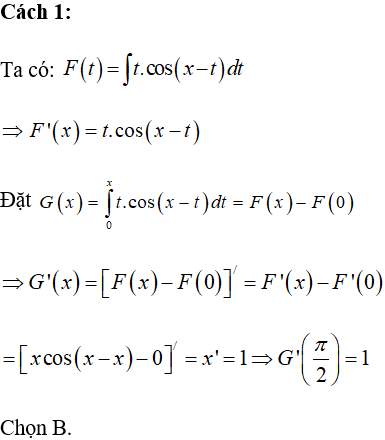
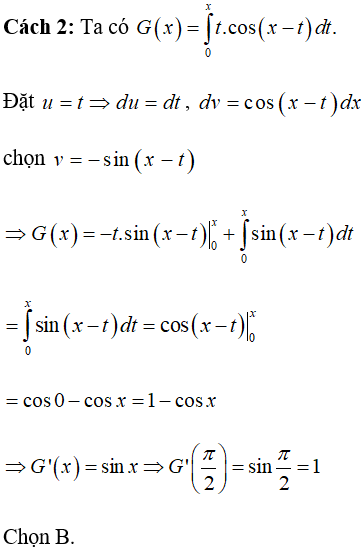
Câu 12: Cho hàm số

Tính G’(x).

A. G'(x) = x².cosx.

B. G'(x) = 2x.cosx.

C. G'(x) = cosx.

D. G'(x) = cosx - 1.

Lời giải:

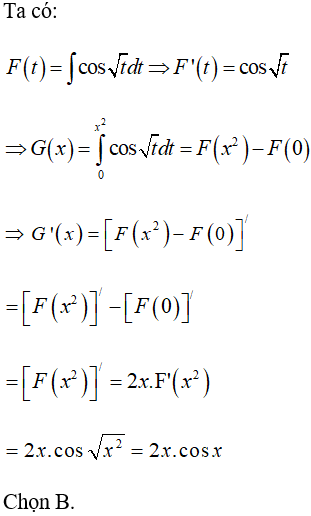
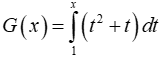
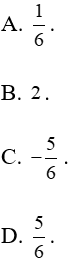
Câu 13: Tìm giá trị nhỏ nhất của trên đoạn [-1;1].

Lời giải:

Câu 14: Cho hàm số

Tính G'(x).

Lời giải:

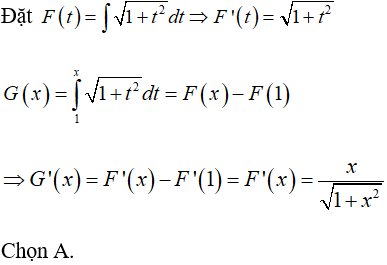
Câu 15: Cho hàm số

Tính G'(x).

Lời giải:

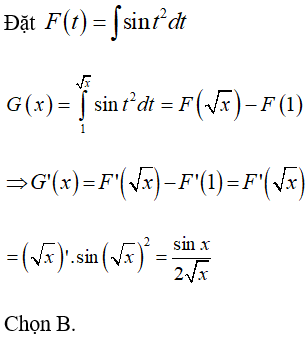
Câu 16: Tính đạo hàm của f(x), biết f(x) thỏa:

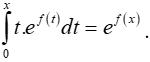
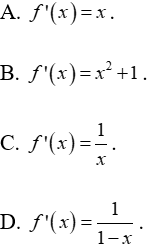
Lời giải: