Cho a, b, c là các số thực dương khác 1 và các hàm số y=log a x, y=log b x, y=log c x

Câu hỏi:

Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số $y = \log_{a} x, y = \log_{b} x, y = \log_{c} x$ . Khẳng định nào sau đây là đúng?

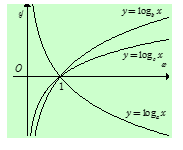
A. a<c<b

B. a<b<c

C. b<a<c

D. b>a>c

Trả lời:

Ta thấy hàm $y = \log_{a} x$ có đồ thị từ trái sang phải theo hướng đi xuống nên là hàm nghịch biến hay 0 < a < 1.

Còn hàm số $y = \log_{b} x$ và $y = \log_{c} x$ là những hàm đồng biến => b,c>1

Từ đó loại được các đáp án C, D

Từ đồ thị hàm số ta thấy tại cùng một giá trị $x_{0} > 1$ thì đồ thị hàm số $y = \log_{b} x$ nằm trên đồ thị hàm số 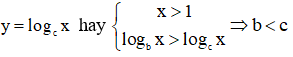hay

Vậy a < b < c

Đáp án cần chọn là: B.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hàm số $y = \log_{\frac{π}{4}} x$ . Khẳng định nào sau đây sai?

Xem lời giải »

Câu 2:

Đồ thị hàm số dưới đây là của hàm số nào?

Xem lời giải »

Câu 3:

Cho các đồ thị hàm số $y = a^{x}, y = b^{x}, y = c^{x} (0 < a, b, c \neq 1)$ . Chọn khẳng định đúng:

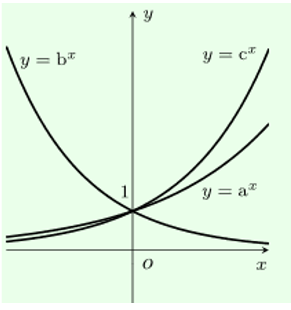
Xem lời giải »

Câu 4:

Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số $y = a^{x}, y = b^{x}, y = c^{x}$ . Khẳng định nào sau đây là đúng?

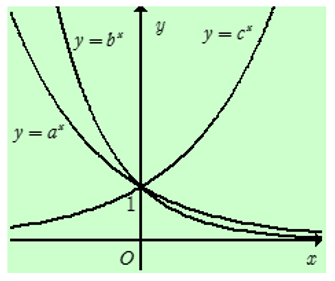
Xem lời giải »

Câu 5:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \log (x^{2} - 2 m x + 4)$ có tập xác định là R.

Xem lời giải »

Câu 6:

Tìm tập giá trị T của hàm số $f (x) = \frac{\ln x}{x}$ với $x \in [1; e^{2}]$

Xem lời giải »

Câu 7:

Biết hai hàm số $y = a^{x}$ và y=f(x) có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng d: y=-x. Tính $f (- a^{3})$

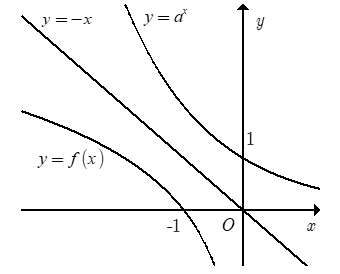
Xem lời giải »

Câu 8:

Cho hàm số $y = 3^{\frac{x}{2}}$ có đồ thị (C). Hàm sô nao sau đây có đồ thị đối xứng với (C) qua đường thẳng y = x.

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho a, b, c là các số thực dương khác 1 và các hàm số y=log a x, y=log b x, y=log c x

Xem thêm bài tập Toán có lời giải hay khác: