Cho a; b là các số thực dương thoả mãn a^2 + b^2 = 14ab . Khẳng định nào sau đây là sai

Câu hỏi:

Cho a; b là các số thực dương thoả mãn a²+ b²= 14ab . Khẳng định nào sau đây là sai ?

A. $\ln \frac{a + b}{4} = \frac{\ln a + \ln b}{2}$

B. 2log₂(a + b) = 4 + log₂a + log₂b.

C. 2log₄(a + b) = 4 + log₄a + log₄b.

D. $2 \log \frac{a + b}{4} = \log a + \log b$

Trả lời:

Chọn C.

Ta có a²+ b²= 14ab nên (a + b)²= 16ab hay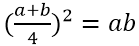

+ Nên ta có 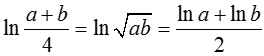vậy A đúng

+ 2log₂( a + b) = log₂ (a + b) ²= log₂( 16ab) = 4 + log₂a + log₂b.

vậy B đúng

+ 2log₄(a + b) = log₄( a + b)²= log₄(16ab) = 2 + log₄a + log₄b . vậy C sai

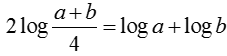+ vậy D đúng.

Câu 1:

Rút gọn $A = \frac{1}{\log_{2} x} + \frac{1}{\log_{3} x} + \frac{1}{\log_{4} x} + . . . + \frac{1}{\log_{2011} x}$

Câu 2:

Kết quả rút gọn của biểu thức $C = \sqrt{\log_{a} b + \log_{b} a + 2} (\log_{a} b - \log_{a b} b) \sqrt{\log_{a} b}$ là:

Câu 3:

Cho a; b > 0, Nếu viết $\log_{5} {(\frac{a^{10}}{\sqrt[6]{b^{5}}})}^{- 0, 2} = x \log_{5} a + y \log_{5} b$ thì xy bằng bao nhiêu ?

Câu 4:

Thu gọn biểu thức $A = \frac{1}{\log_{a} b} + \frac{1}{\log_{a^{2}} b} + \frac{1}{\log_{a^{3}} b} + . . . + \frac{1}{\log_{a^{n}} b}$ ta được:

Câu 5:

Với giá trị nào của m thì biểu thức $f (x) = \log_{\sqrt{5}} (x - m)$ xác định với mọi $x \in (- 3; + \infty)$ ?

Câu 6:

Biểu thức ln( x²- 2mx + 4) có nghĩa với mọi x khi

Câu 7:

Tìm x để ba số ln2; ln( 2^x- 1); ln( 2^x + 3) theo thứ tự lập thành cấp số cộng.

Câu 8:

Biểu thức T = log₂( ax²- 4x + 1) có nghĩa với mọi x khi

Các dạng bài tập Toán lớp 12