Cho các hàm số y = 3x - 2 (d1); y = -x + 6 (d2)
Câu hỏi:
Cho các hàm số y = 3x – 2 (d1); y = −x + 6 (d2).
a) Vẽ các đường thẳng (d1), (d2) trên cùng một mặt phẳng tọa độ.
b) Gọi A, B, C lần lượt là giao điểm của (d1), (d2); (d1) với trục hoành; (d2) với trục hoành
Tính chu vi và diện tích tam giác ABC.
Trả lời:
a) Vẽ đồ thị hàm số
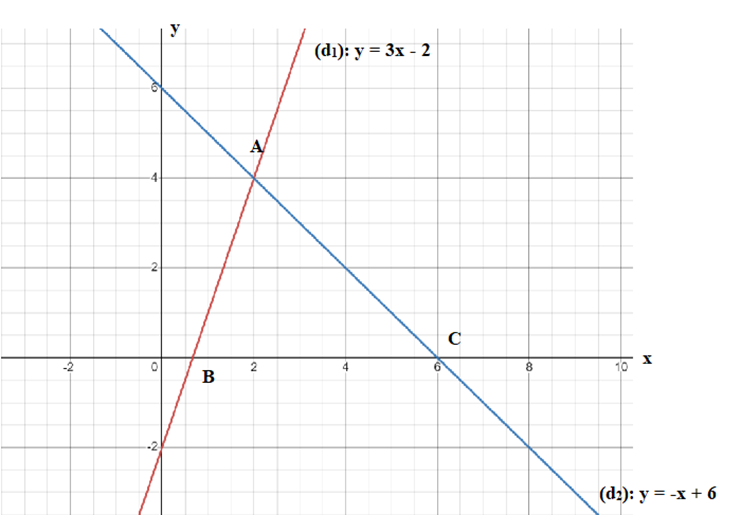
+ (d1) cắt Oy tại điểm có tọa độ (0; a)
Thay vào phương trình d1 có: 3.0 – 2 = y
Suy ra: (d1) cắt Oy tại điểm (0; –2)
+ (d2) cắt Oy tại điểm (0; 6)
Xét phương trình hoành độ giao điểm d1 và d2 có:
3x – 2 = –x + 6
4x = 8
x = 2
⇒ y = 3.2 – 2 = 4
Nên d1 cắt d2 tại A(2; 4)
Vẽ được đồ thị hàm số d1 qua 2 điểm là A(2; 4) và (0; –2)
Vẽ được đồ thị hàm số d2 qua 2 điểm là A(2; 4) và (0; 6).
b) d1 cắt Ox tại điểm \(\left( {\frac{2}{3};0} \right)\)
d2 cắt Ox tại điểm (6; 0)
Suy ra: A(2; 4), B\(\left( {\frac{2}{3};0} \right)\); C(6; 0)
AB = \(\sqrt {{{\left( {\frac{2}{3} - 2} \right)}^2} + {{\left( {0 - 4} \right)}^2}} = \frac{{4\sqrt {10} }}{3}\)
AC = \(\sqrt {{{\left( {6 - 2} \right)}^2} + {{\left( {0 - 4} \right)}^2}} = 4\sqrt 2 \)
BC = \(\sqrt {{{\left( {6 - \frac{2}{3}} \right)}^2} + {0^2}} = \frac{{16}}{3}\)
Chu vi tam giác ABC = AB + AC + BC = \(\frac{{4\sqrt {10} }}{3} + 4\sqrt 2 + \frac{{16}}{3}\)
Đường cao hạ từ A xuống BC = yA = 4 (đơn vị độ dài)
SABC = \(\frac{1}{2}.4.\frac{{16}}{3} = \frac{{32}}{3}\)(đvdt).

