Cho đường tròn (O) đường kính AB. Đường thẳng d tiếp xúc với
Câu hỏi:
Cho đường tròn (O) đường kính AB. Đường thẳng d tiếp xúc với (O) tại A. Gọi I là một điểm cố định trên đoạn thẳng AB. Gọi DE là dây cung thay đổi của (O) luôn đi qua I. Gọi BD, BE cắt d lần lượt tại M, N.
1) Chứng minh rằng tứ giác DENM là tứ giác nội tiếp.
2) Chứng minh rằng tích AM. AN không đổi.
3) Chứng minh rằng tâm đường tròn ngoại tiếp tứ giác DENM thuộc một đường thẳng cố định.
Trả lời:
1) Ta có: AB là đường kính của (O) nên AD ⊥ BM, AE ⊥ EB
Mà AB ⊥ MN
Nên BD.BM = BA2 = BE. BN
⇒ \(\frac{{BD}}{{BN}} = \frac{{BE}}{{BM}}\)
Mà \(\widehat {DBE} = \widehat {MBN}\)
⇒ ∆BDE ∽ ∆BNM (c.g.c.)
⇒ \(\widehat {BDE} = \widehat {BNM}\)
⇒ MNED nội tiếp
2) Vẽ đường tròn ngoại tiếp ΔBMN, (BMN) ∩ AB = P
⇒ ΔBEI ∽ ΔBPN(g.g)
⇒ \(\frac{{BE}}{{BP}} = \frac{{BI}}{{BN}}\)
⇒ BI.BP = BE.BN = BA2
⇒ BP = \(\frac{{B{A^2}}}{{BI}}\)⇒ P cố định
Mà \(\widehat {PAN} = \widehat {MAB},\widehat {APN} = \widehat {BPN} = \widehat {BMN} = \widehat {BMA}\)
⇒ ΔABM ∽ ΔANP(g.g)
⇒ \(\frac{{AM}}{{AP}} = \frac{{AB}}{{AN}}\)
⇒ AM.AN = AB. AP không đổi
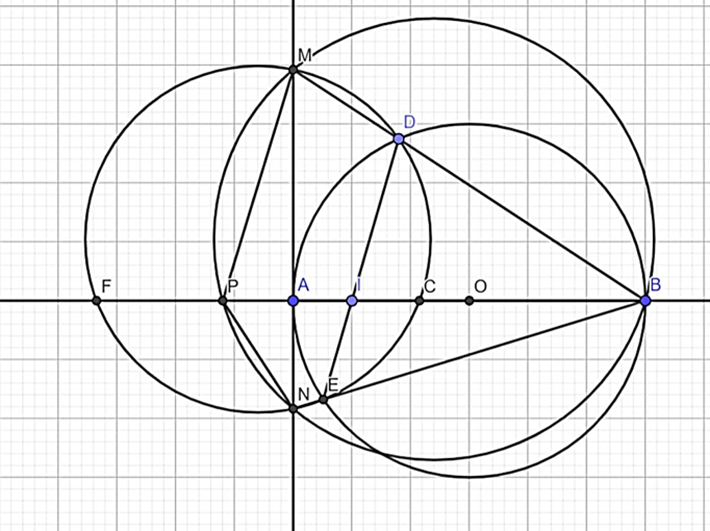
3.Vẽ đường tròn ngoại tiếp DMNE, (DMNE) ∩ AB = C, F (như hình vẽ)
Chứng minh tương tự câu 2 có AF.AC = AM.AN ⇒ AF.AC = AP.AB
Lại có BCF, BDM là cát tuyến tại B với (DMNE)
⇒ BC.BF = BD.BM = BA2
⇒ \(\left\{ \begin{array}{l}BC.BF = B{A^2}\\AF.AC = AP.AB\end{array} \right.\)
⇒ \(\left\{ \begin{array}{l}\left( {AB - AC} \right)\left( {AB + AF} \right) = B{A^2}\\AF.AC = AP.AB\end{array} \right.\)
⇒ \(\left\{ \begin{array}{l}A{B^2} + AB\left( {AF - AC} \right) - AF.AC = B{A^2}\\AF.AC = AP.AB\end{array} \right.\)
⇒ \(\left\{ \begin{array}{l}AB\left( {AF - AC} \right) = AF.AC\\AF.AC = AP.AB\end{array} \right.\)
⇒ \(\left\{ \begin{array}{l}AB\left( {AF - AC} \right) = AP.AB\\AF.AC = AP.AB\end{array} \right.\)
⇒ \(\left\{ \begin{array}{l}AF - AC = AP\\AF.AC = AP.AB\end{array} \right.\)
⇒ \(\left\{ \begin{array}{l}AF = AC + AP\\AF.AC = AP.AB\end{array} \right.\)
⇒\(\left\{ \begin{array}{l}AF = AC + AP\\A{C^2} + AC.AP - AP.AB = 0\end{array} \right.\) ⇒ C cố định
⇒ C, F cố định
⇒ Tâm (DENM) thuộc trung trực của CF cố định.

