Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Qua A kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Vẽ tia Ax nằm giữa tia AB và tia AO
Câu hỏi:
Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Qua A kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Vẽ tia Ax nằm giữa tia AB và tia AO cắt đường tròn (O) tại hai điểm C và D (C nằm giữa A và D). Gọi M là trung điểm của dây CD, kẻ BH vuông góc với AO tại H.
a, Tính tích OH.OA theo R.
b, Chứng minh 4 điểm A, B, M, O cùng thuộc một đường tròn.
c, Gọi E là giao điểm của OM với HB. Chứng minh ED là tiếp tuyến của đường tròn (O;R).
Trả lời:
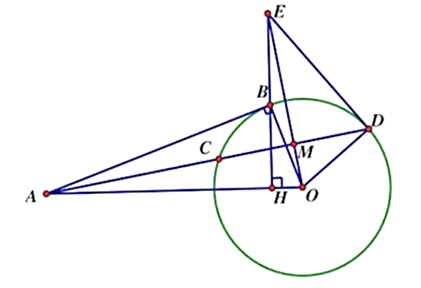
a) Xét tam giác AMO vuông tại A có AH vuông góc MO
Áp dụng hệ thức lượng: OH.OM = OA2 = R2
b) Xét (O) có M là trung điểm CD nên OM vuông góc CD (bán kính vuông góc dây cung)
⇒
Lại có: BA là tiếp tuyến nên
Suy ra: M, B thuộc đường tròn đường kính OA
Hay A, B, M, O cùng thuộc một đường tròn.
c) Xét tam giác OHE và tam giác OMA có:
Chung
⇒ ∆OHE ∽ ∆OMA (g.g)
⇒
Suy ra:
Xét tam giác ODE và tam giác OMD có:
Chung
⇒ ∆ODE ∽ ∆OMD (c.g.c)
⇒
Suy ra: OD ⊥ ED mà D thuộc (O) nên ED là tiếp tuyến của (O).

