Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E.
Câu hỏi:
Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng:
a) Hai cung nhỏ CF và BD bằng nhau.
b) Hai cung nhỏ BF và DE bằng nhau.
c) DE = BF.
Trả lời:
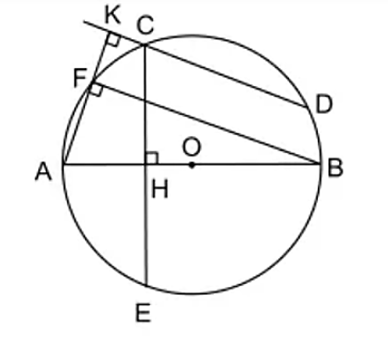
a) Tam giác AFB nội tiếp đường tròn (O) có AB là đường kính nên tam giác AFB vuông tại F
⇒
⇒ BF ⊥ AK tại F
Mà AK vuông góc với CD (gt)
⇒ BF // CD
⇒ (hai cung chắn giữa hai dây song song thì bằng nhau).
b) Đường kính AB vuông góc với CE tại H nên H là trung điểm của CE
Do đó, C đối xứng với E qua trục AB
⇒ BC = BE
⇒ (hai dây cung bằng nhau căng hai cung bằng nhau)
Mà (cmt)
⇒
c) Có: (cmt)
Do đó, BF = DE (hai cung bằng nhau căng hai dây bằng nhau).