Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC.
Câu hỏi:
Cho góc . Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) DEAB = DECD.
c) OE là tia phân giác của góc xOy.
Trả lời:
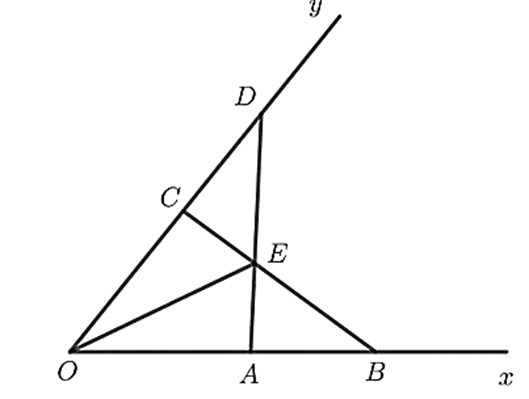
a) Xét tam giác OAD và tam giác OCB có:
OA = OC (giả thiết)
chung
OD = OB
Do đó: ∆OAD = ∆OCB (c.g.c)
Suy ra: AD = BC
b) Do OA = PC, OB = OD nên OB – OA = OD – OC hay AB = CD
Do ∆OAD = ∆OCB (c.g.c) nên
là góc ngoài tại định C của tam giác OBC nên
là góc ngoài tại định C của tam giác OAD nên
Từ (1) và (2) suy ra:
Xét tam giác EAB và ECD có:
AB = CD
Do đó: ∆EAB = ∆ECD (g.c.g)
c) Do ∆EAB = ∆ECD (g.c.g) nên BE = DE
Xét tam giác ODE và OBE có:
OD = OB
OE chung
BE = DE
Do đó: ∆ODE = ∆OBE (c.c.c)
Suy ra:
Vậy OE là tia phân giác của
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a)
b) Tứ giác OKME là hình chữ nhật.
c) P, O, N thẳng hàng và KE // PN.
Xem lời giải »
Câu 2:
Cho đa thức R(x) = x2 – 2x. Tính giá trị biểu thức
Xem lời giải »
Câu 3:
Rút gọn biểu thức: (4x – 1)3 - (4x − 3)(16x2 + 3).
Xem lời giải »
Câu 4:
Cho tam giác ABC. Hai điểm M và N di chuyển sao cho . Chứng minh MN luôn đi qua một điểm cố định.
Xem lời giải »
Câu 5:
cho hình bình hành ABCD, đường chéo AC lớn hơn đường chéo BD, kẻ CH vuông góc với AD, CK vuông góc với AB.
a, Chứng minh tam giác BCK đồng dạng tam giác DCH.
b, Chứng minh tam giác CKH đồng dạng tam giác BCA.
c, Chứng minh HK = AC.sin
d, Tính diện tích của tứ giác AKCH nếu , AB = 4cm, AC = 5cm.
Xem lời giải »
Câu 6:
Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ
Xem lời giải »
Câu 7:
Cho tam giác ABC có M là trung điểm của cạnh BC. Vẽ các điểm F, E, G sao cho B, M, C theo thứ tự là trung điểm của AF, AE và AG. Chứng minh ba điểm F, E, G thẳng hàng.
Xem lời giải »
Câu 8:
Cho tam giác ABC nhọn đường cao AH. E, F là hình chiếu của H lên AB, AC. Khi SAHE = 4cm2, SBHE = 1cm2. Tính AB biết EH = 2 cm.
Xem lời giải »


