Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ .
Câu hỏi:
Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ
Trả lời:
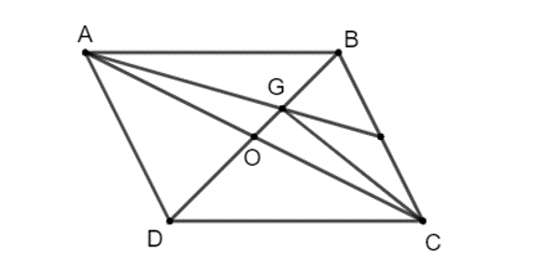
Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD.
Khi đó O là trung điểm của AC và BD.
Do đó BO là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên G thuộc trung tuyến BO của tam giác ABC.
Theo tính chất trọng tâm ta có:
Mà nên
Hai vectơ cùng hướng và nên
Ta có:
Do ABCD là hình bình hành nên
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a)
b) Tứ giác OKME là hình chữ nhật.
c) P, O, N thẳng hàng và KE // PN.
Xem lời giải »
Câu 2:
Cho đa thức R(x) = x2 – 2x. Tính giá trị biểu thức
Xem lời giải »
Câu 3:
Rút gọn biểu thức: (4x – 1)3 - (4x − 3)(16x2 + 3).
Xem lời giải »
Câu 4:
Cho tam giác ABC. Hai điểm M và N di chuyển sao cho . Chứng minh MN luôn đi qua một điểm cố định.
Xem lời giải »
Câu 5:
Cho tam giác ABC có M là trung điểm của cạnh BC. Vẽ các điểm F, E, G sao cho B, M, C theo thứ tự là trung điểm của AF, AE và AG. Chứng minh ba điểm F, E, G thẳng hàng.
Xem lời giải »
Câu 6:
Cho tam giác ABC nhọn đường cao AH. E, F là hình chiếu của H lên AB, AC. Khi SAHE = 4cm2, SBHE = 1cm2. Tính AB biết EH = 2 cm.
Xem lời giải »
Câu 7:
Cho ∆ ABC nhọn, đường cao AH. Kẻ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC).
a) Chứng minh: ∆AEH ∽ ∆AHB. Từ đó suy ra AH2 = AE.AB.
b) Chứng minh AE. AB = AF.AC.
c) Cho chu vi các ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm. Tính diện tích ∆AEF và ∆ACB biết diện tích ∆ACB lớn hơn diện tích ∆AEF là 25 cm2.
Xem lời giải »
Câu 8:
Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC
a) Chứng minh
b) Chứng minh
Xem lời giải »


