Cho hai đường tròn (O; R) và (O'; R') (R > R') tiếp xúc ngoài nhau tại A. Qua A kẻ hai cát tuyến BD và CE (B, C ∈ (O')); D, E ∈ (O)). Chứng minh
Câu hỏi:
Trả lời:
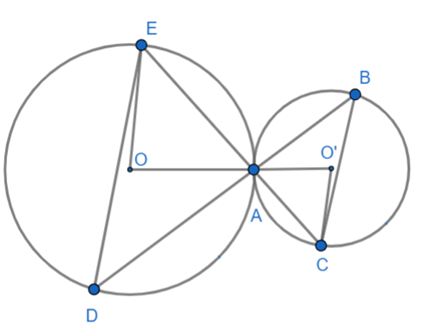
Xét tam giác O'AC có O'A = O'C = R' nên tam giác O'AC cân tại O'
Suy ra:
Tương tự: tam giác OAE cân tại O nên:
Mà là 2 góc đối đỉnh nên
Suy ra:
Xét tam giác O'CA và OAE có:
⇒ ∆O'AC ∽ ∆OAE (c.g.c)
Suy ra:
Mà: (vì là góc ở tâm, chắn cung , )
Và (vì là góc ở tâm, chắn cung , )
Suy ra: .

