Cho hai số thực a , b thỏa điều kiện ab = 1, a + b ≠ 0. Tính giá trị của biểu thức:
Câu hỏi:
Cho hai số thực a , b thỏa điều kiện ab = 1, a + b ≠ 0. Tính giá trị của biểu thức:
Trả lời:
Với ab = 1, a + b ≠ 0 ta có:
Vậy P = 1
Câu hỏi:
Cho hai số thực a , b thỏa điều kiện ab = 1, a + b ≠ 0. Tính giá trị của biểu thức:
Trả lời:
Với ab = 1, a + b ≠ 0 ta có:
Vậy P = 1
Câu 3:
Cho tam giác ABC cân tại A, đường cao AD, K là trung điểm của AD. Gọi I là hình chiếu của điểm D trên CK. Chứng minh rằng .
Câu 5:
Cho hai tập hợp E = (2;5] và F = [2m - 3; 2m + 2]. Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.
Câu 6:
Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.
Câu 7:
Cho hàm số y = x – 2 có đồ thị là đường thẳng (d).
a, Vẽ đồ thị hàm số đã cho.
b, Gọi A, B lần lượt là giao điểm của (d) với Ox, Oy. Tính diện tích tam giác OAB (đơn vị đo trên các trục tọa độ centimet).
c, Tìm giá trị của m để đường thẳng (d) và đường thẳng (d1): y = -2x + m² - 3 cắt nhau tại một điểm trên trục tung.
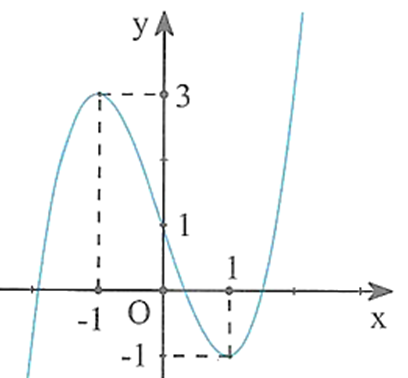
Câu 8:
Cho hàm số f(x) hàm số y = f'(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Với giá trị nào của tham số m thì phương trình f(x) = 3x + m có nghiệm thuộc khoảng (-1;1).