Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Một cát tuyến
Câu hỏi:
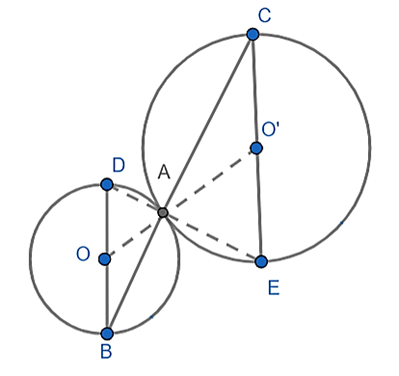
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Một cát tuyến kẻ qua A cắt đường tròn (O) ở B, cắt đường tròn (O') ở C. Kẻ các đường kính BD và CE của hai đường tròn (O) và (O'). Chứng minh \(\widehat {ADB} = \widehat {AEC}\)
Trả lời:
Có: \(\widehat {BAD} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn (O))
\(\widehat {CAE} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn (O'))
Suy ra: \(\widehat {BAD} + \widehat {CAE} = 90^\circ + 90^\circ = 180^\circ \).
Do đó: D, A, E thẳng hàng.
Ta có: tam giác AOD cân tại O vì OD = OA
Suy ra: \(\widehat {OAD} = \widehat {ODA}\)
Tam giác O'AE cân tại O' vì O'A = O'E
⇒ \(\widehat {O'AE} = \widehat {O'EA}\)
Mà: \(\widehat {OAD} = \widehat {O'AE}\)(2 góc đối đỉnh) do đó BD // CE
Suy ra: \(\widehat {ADB} = \widehat {AEC}\) (2 góc so le trong).

