Cho hai số thực a; b với 1< a< b. Khẳng định nào sau đây là khẳng định đúng

Câu hỏi:

Cho hai số thực a; b với 1< a< b. Khẳng định nào sau đây là khẳng định đúng?

A. log_ab < 1 < log_ba

B. b < loga1 < log ba

C. log_ab < log_ba < 1

D. log_ba < 1 < log_ab

Trả lời:

Chọn D.

Từ giả thiết 1 < a < b ta có 0 < log_aa < log_ab hay 1 < log_ab .

Áp dụng công thức đổi cơ số thì 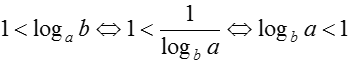vì log_ba > 1 nên ta có: log_ba < 1 < log_ab.

Câu 1:

Rút gọn $A = \frac{1}{\log_{2} x} + \frac{1}{\log_{3} x} + \frac{1}{\log_{4} x} + . . . + \frac{1}{\log_{2011} x}$

Câu 2:

Kết quả rút gọn của biểu thức $C = \sqrt{\log_{a} b + \log_{b} a + 2} (\log_{a} b - \log_{a b} b) \sqrt{\log_{a} b}$ là:

Câu 3:

Cho a; b > 0, Nếu viết $\log_{5} {(\frac{a^{10}}{\sqrt[6]{b^{5}}})}^{- 0, 2} = x \log_{5} a + y \log_{5} b$ thì xy bằng bao nhiêu ?

Câu 4:

Thu gọn biểu thức $A = \frac{1}{\log_{a} b} + \frac{1}{\log_{a^{2}} b} + \frac{1}{\log_{a^{3}} b} + . . . + \frac{1}{\log_{a^{n}} b}$ ta được:

Câu 5:

Cho a; b > 0 thỏa mãn a²+ b ²= 7ab. Chọn mệnh đề đúng trong các mệnh đề sau?

Câu 6:

Cho x; y; z là các số thực dương tùy ý khác 1 và xyz khác 1. Đặt a = log_xy; b = log_zy. Mệnh đề nào sau đây đúng?

Câu 7:

Cho các số dương a; b thõa mãn 4a²+ 9b²= 13ab . Chọn câu trả lời đúng.

Câu 8:

Cho x; y > 0 và x²+ 4y²= 12xy . Khẳng định nào sau đây là khẳng định đúng?

Các dạng bài tập Toán lớp 12