Cho hàm số đa thức f(x) có đạo hàm trên R. Biết f(0) = 0 và đồ thị hàm số y = f’(x)
Câu hỏi:
Cho hàm số đa thức f(x) có đạo hàm trên R. Biết f(0) = 0 và đồ thị hàm số y = f’(x) như hình sau:
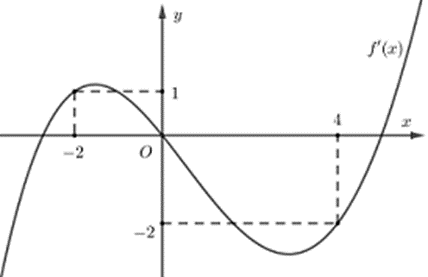
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2}} \right|\) đồng biến trên khoảng nào dưới đây?
A.(4; +∞)
B. (0; 4)
C. (–∞; –2)
D. (–2; 0).
Trả lời:
Đáp án đúng là: B
Đặt h(x) = 4f(x) + x2
Ta có: \(h'(x) = 4f(x) + 2x = 4\left[ {f'(x) + \frac{x}{2}} \right]\)
Số nghiệm của phương trình h’(x) = 0 là số giao điểm của đồ thị hàm số y = f’(x) và đường thẳng \(y = - \frac{x}{2}\)
Vẽ đồ thị hàm số y = f’(x) và đường thẳng \(y = - \frac{x}{2}\) trên cùng mặt phẳng tọa độ ta có:
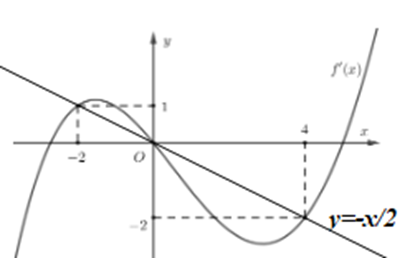
Dựa vào đồ thị hàm số ta thấy \(h'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = 0}\\{x = 4}\end{array}} \right.\)
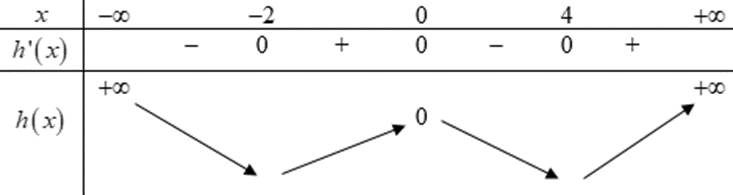
Khi đó ta có BBT hàm số y = h(x):
Khi đó ta suy ra được BBT hàm số g(x) = |h(x)| như sau:
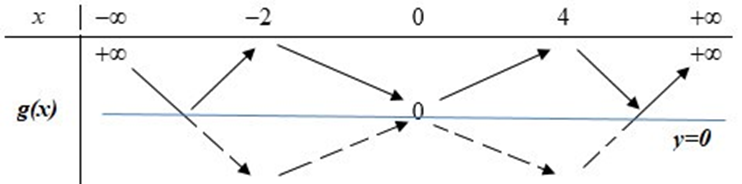
Dựa vào BBT ta thấy hàm số g(x) đồng biến trên (0; 4)
Vậy đáp án cần chọn là: B.

