Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình log căn bậc hai 2
Câu hỏi:
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \right)\) có hai nghiệm thực phân biệt?
A.3
B. vô số
C. 4
D. 5
Trả lời:
Đáp án đúng là: A
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{x > 1}\\{mx > 8}\end{array}} \right.\)
Ta có: \({\log _{\sqrt 2 }}\left( {x - 1} \right) = {\log _2}\left( {mx - 8} \right)\) (1)
\( \Leftrightarrow {\log _2}{(x - 1)^2} = {\log _2}(mx - 8)\)
\(\begin{array}{l} \Leftrightarrow {(x - 1)^2} = mx - 8\\ \Leftrightarrow {x^2} - 2x + 9 = m\\ \Leftrightarrow x - 2 + \frac{9}{x} = m{\rm{ }}\left( 2 \right)\end{array}\)
Phương trình (1) có 2 nghiệm thực phân biệt
⇔ Phương trình (2) có 2 nghiệm thực phân biệt lớn hơn 1
Xét hàm số \(f(x) = x - 2 + \frac{9}{x},x > 1\) có \(f'(x) = 1 - \frac{9}{{{x^2}}},f'(x) = 0 \Leftrightarrow x = 3\)
Bảng biến thiên:
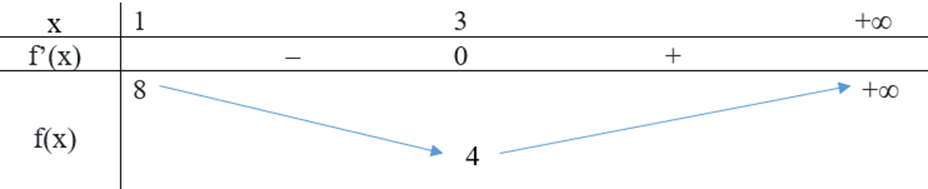
Phương trình (2) có 2 nghiệm thực phân biệt lớn hơn 1 \( \Leftrightarrow 4 < m < 8\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \{ 5;6;7\} \)
Do đó 3 giá trị của m thỏa mãn
Vậy ta chọn đáp án A.

