Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH. Chứng minh: a) ΔAHF = ΔADC. b) AC ⊥ HF.
Câu hỏi:
Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH. Chứng minh:
a) ΔAHF = ΔADC.
b) AC ⊥ HF.
Trả lời:
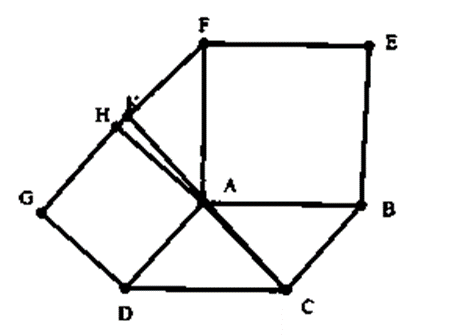
Gọi K là giao điểm của AC và HF
a) Do ABEF và ADGH đều là hình vuông nên
AH = BA, AH = DA
Do ABCD là hình bình hành nên BA=DC.
Suy ra AF = DC
Ta chứng minh được và
Suy ra
Xét hai tam giác HAF và ADC, ta có:
AH = DA
AF = DA
Suy ra ΔHAF = ΔADC (c.g.c)
b) Ta có: và nên
Mà (vì ΔHAF = ΔADC), suy ra
Trong tam giác AHK, ta có:
Suy ra
Vậy AK ⊥ HK hay AC ⊥ HF.