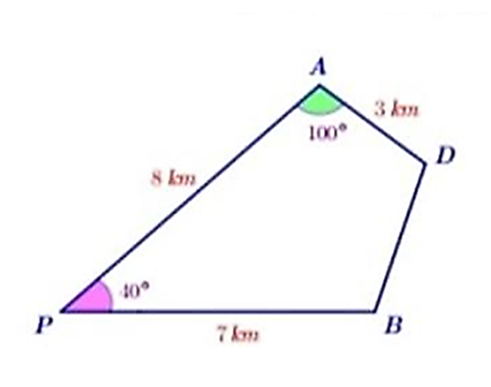
Cho tam giác nhọn ABC. Vẽ ra phía ngoài của tam giác này các tam giác ABD và tam giác ACE vuông cân tại A. Gọi M là trung điểm của DE.
Câu hỏi:
Cho tam giác nhọn ABC. Vẽ ra phía ngoài của tam giác này các tam giác ABD và tam giác ACE vuông cân tại A. Gọi M là trung điểm của DE. Chứng minh rằng hai đường thẳng MA và BC vuông góc với nhau.
Trả lời:
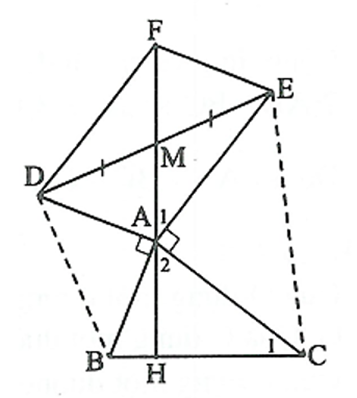
Vẽ hình bình hành DAEF. Khi đó AF đi qua M.
Gọi H là giao điểm của MA với BC.
Ta có: EF = AD = AB.
mà nên
Xét tam giác AEF và CAB có:
AC = AE
AB = AF
⇒ ΔAEF = ΔCAB (g.c.g)
⇒
Lại có:
Suy ra:
Do đó: AM vuông góc BC.