Cho tứ giác ABCD. M, N là trung điểm của AC và BD. Chứng minh: AB2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4MN2.

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho tứ giác ABCD. M, N là trung điểm của AC và BD.

Chứng minh: AB²+ BC² + CD² + DA² = AC² + BD² + 4MN².

Trả lời:

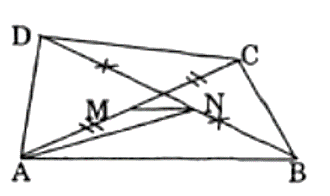
Cho tứ giác ABCD. M, N là trung điểm của AC và BD. Chứng minh: AB2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4MN2. (ảnh 1)

Trong tam giác ABD ta có AN là đường trung tuyến:

$A N^{2} = \frac{A B^{2} + A D^{2}}{2} - \frac{B D^{2}}{4}$

⇒ AB² + AD² = 2AN² + $\frac{B D^{2}}{2}$ (1)

Trong tam giác CBD có CN là đường trung tuyến:

$C N^{2} = \frac{C D^{2} + C B^{2}}{2} - \frac{B D^{2}}{4}$

⇒ CB² + CD² = 2CN² + $\frac{B D^{2}}{2}$ (2)

Cộng (1) với (2) ta được: AB² + AD² + CB² + CD² = 2AN² + 2CN² + BD²(3)

Xét tam giác CAN có NM là trung tuyến:

$M N^{2} = \frac{C N^{2} + A N^{2}}{2} - \frac{A C^{2}}{4}$

⇒ AN² + CN² = 2MN² + $\frac{A C^{2}}{2}$ (4)

Thay (4) vào (3) ta được:

AB² + AD² + CB² + CD² = 2.(2MN² + $\frac{A C^{2}}{2}$ ) + BD² = 4MN² + AC² + BD²

Vậy B²+ BC² + CD² + DA² = AC² + BD² + 4MN².

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:

a) $\overset{⏜}{A P} = \overset{⏜}{B N}$

b) Tứ giác OKME là hình chữ nhật.

c) P, O, N thẳng hàng và KE // PN.

Xem lời giải »

Câu 2:

Cho đa thức R(x) = x² – 2x. Tính giá trị biểu thức $S = \frac{1}{R (3)} + \frac{1}{R (4)} + ... + \frac{1}{R (2022)} + \frac{1}{R (2023)}$

Xem lời giải »

Câu 3:

Rút gọn biểu thức: (4x – 1)³ - (4x − 3)(16x² + 3).

Xem lời giải »

Câu 4:

Cho tam giác ABC. Hai điểm M và N di chuyển sao cho $\vec{M N} = 2 \vec{M A} - \vec{M B} + \vec{M C}$ . Chứng minh MN luôn đi qua một điểm cố định.

Xem lời giải »

Câu 5:

Cho tam giác nhọn ABC. Vẽ ra phía ngoài của tam giác này các tam giác ABD và tam giác ACE vuông cân tại A. Gọi M là trung điểm của DE. Chứng minh rằng hai đường thẳng MA và BC vuông góc với nhau.

Xem lời giải »

Câu 6:

Hai bạn An và Hưng cùng xuất phát từ điểm P, đi theo hai hướng khác nhau và tạo với nhau một góc 40° để đến đích là điểm D. Biết rằng họ dừng lại để ăn trưa lần lượt tại A và B (như hình vẽ minh hoạ). Hỏi Hưng phải đi bao xa nữa để đến được đích?