Cho hình bình hành ABCD. Vẽ AE ⊥ BC tại E, DF ⊥ AB tại F. Biết AE = DF. Chứng minh rằng tứ giác ABCD là hình thoi.
Câu hỏi:
Cho hình bình hành ABCD. Vẽ AE ⊥ BC tại E, DF ⊥ AB tại F. Biết AE = DF. Chứng minh rằng tứ giác ABCD là hình thoi.
Trả lời:
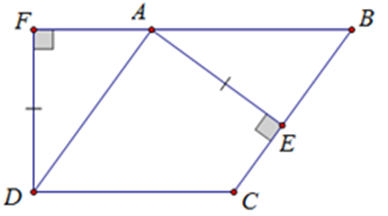
Ta có: (vì AD // BC)
Xét tam giác AFD và tam giác BEA có:
DF = AE (giả thiết)
Suy ra: ∆AFD = ∆BEA (g.c.g)
⇒ AD = AB (2 cạnh tương ứng)
Xét hình bình hành ABCD có AD = AB nên ABCD là hình thoi.

