Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD
A.
B.
C.
D.
Trả lời:
Chọn D
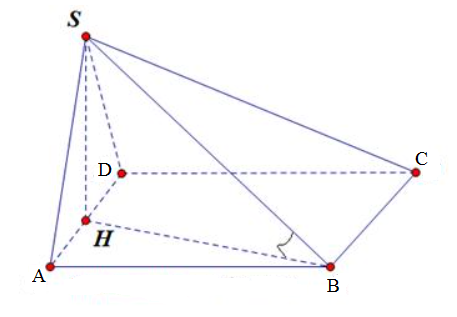
Gọi H là trung điểm của AD
Ta có cân tại S nên
Xét vuông tại A, ta có: (định lý Py - ta - go)
Ta lại có:
Xét vuông tại H, ta có:
Thể tích của hình chóp SABCD là:
Câu 5:
Cho lăng trụ ABC.A'B'C' có độ dài cạnh bên bằng 2a, đáy ABC là tam giác đều cạnh a và hình chiếu vuông góc của đỉnh A’ trên mặt phẳng (ABC) là trung điểm cạnh BC. Thể tích khối chóp A.BCC’B’ là:
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC=a, SA = SB = SC = 3a. Góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp G.ABC là:
Câu 7:
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. SA = 2AD = 2a. Góc giữa mp(SBC) và mặt đáy là 45o. Gọi M là trung điểm của BC. Khoảng cách từ M đến mp(SBD) là:
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là . Tính thể tích khối chóp S.ABCD
