Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SB
Câu hỏi:
Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SB. Gọi E, F là hai điểm lần lượt thuộc miền trong tam giác ABD và tam giác BCD. Tìm giao tuyến của mặt phẳng (MEF) và mặt phẳng (SCD).
Trả lời:
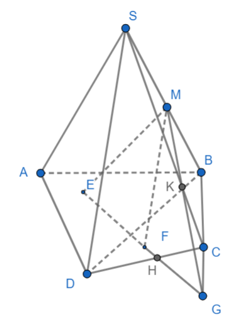
Vì E,F lần lượt nằm ở miền trong của ABD, BCD nên EF ⊂ (ABCD)
Trong (ABCD) ta cho EF cắt CD, BC lần lượt tại H,G
Ta có H ∈ CD
⇒ H ∈ (MEF) ∩ (SCD)
Trong (SBC), ta có MG ⊂ (SCD), SC ⊂ (SCD) nên MG cắt SC tại K
⇒ K ∈ (SCD) ∩ (MEF) do K ∈ MG ⊂ (MEF)
Vậy (SCD) ∩ (MEF) = KH

