Cho hình chữ nhật ABCD có cạnh AD = a, M là trung điểm
Câu hỏi:
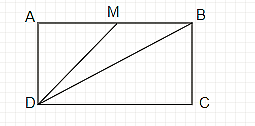
Cho hình chữ nhật ABCD có cạnh AD = a, M là trung điểm của cạnh AB. Biết rằng sin\(\widehat {MDB} = \frac{1}{3}\). Tính độ dài của đoạn thẳng AB theo a.
Trả lời:
Ta có: cos\(\widehat {MDB} = \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} = \frac{{2\sqrt 2 }}{3}\)
Xét tam giác AMD có: SAMD = \(\frac{1}{2}\)AD.AM
SAMD = \(\frac{1}{2}.AD.\frac{{AB}}{2} = \frac{1}{4}.AD.AB = \frac{1}{4}.AD.a\)
Xét tam giác MDB có: SBMD = \(\frac{1}{2}\)MD.DB.sin\(\widehat {MDB} = \frac{1}{6}.MD.DB\)
Xét tam giác ABD có: SABD = \(\frac{1}{2}\)AD.AB = \(\frac{1}{2}.a.AB\) (1)
Mà SAMD + SBMD = SABD
⇔ \(\frac{1}{4}.a.AB + \frac{1}{6}.MD.DB = \frac{1}{2}.a.AB\)
Xét tam giác MDB có: MB2 = MD2 + DB2 – 2.MB.BD.cos\(\widehat {MDB}\)
⇔ \(\frac{{A{B^2}}}{4} = M{D^2} + D{B^2} - 2.MB.BD.\frac{{2\sqrt 2 }}{3}\)
⇔ MD.DB = \(\left( {M{D^2} + D{B^2} - \frac{{A{B^2}}}{4}} \right).\frac{3}{{4\sqrt 2 }}\)
⇔ MD.DB = \(\left( {2{a^2} + A{B^2}} \right).\frac{3}{{4\sqrt 2 }}\left( 2 \right)\)
Thế (2) vào (1) ta có:
\(\frac{1}{4}a.AB + \frac{{\sqrt 2 }}{{16}}\left( {2{a^2} + A{B^2}} \right) = \frac{1}{2}.AB.a\)
⇔ \(\frac{{\sqrt 2 }}{{16}}\left( {2{a^2} + A{B^2}} \right) = \frac{1}{4}a.AB\)
⇔ AB2 – 2\(\sqrt 2 \)a.AB + 2a2 = 0
⇔ (AB – a\(\sqrt 2 \))2 = 0
⇔ AB = a\(\sqrt 2 \).

