Cho hình thang cân ABCD (AD // BC). Biết AB = 12cm, AC = 16cm
Câu hỏi:
Cho hình thang cân ABCD (AD // BC). Biết AB = 12cm, AC = 16cm, BC = 20 cm. Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Trả lời:
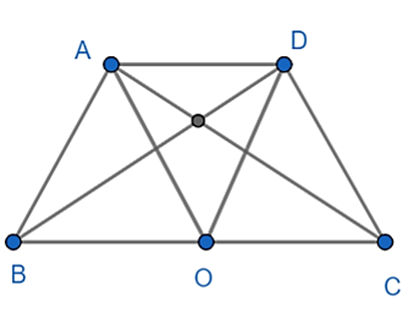
Xét tam giác ABC thấy BC2 = AC2 + AB2 (202 = 162 + 122)
Nên tam giác ABC vuông tại A
Gọi O là trung điểm BC
Nên OB = OC
Vì tam giác ABC vuông tại A nên OA = \(\frac{1}{2}BC = OB = OC\) (1)
Lại có: ABCD là hình thang cân nên AC = BD; AB = DC (tính chất)
⇒ BD = 16cm, DC = 12cm
Lại có: BD2 + DC2 = BC2 (do 202 = 162 + 122)
Nên ∆BDC vuông tại D.
Suy ra: \(OD = \frac{1}{2}BC = OB = OC\) (2)
Từ (1) và (2): OA = OB = OC = OD
Vậy A, B, C, D cùng thuộc đường tròn tâm O, bán kính R = OA.
R = OA= \(\frac{1}{2}BC = \frac{1}{2}.20 = 10\left( {cm} \right)\)
Vậy bán kính của đường tròn ngoại tiếp ABCD bằng 10 cm.

