Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD.
Câu hỏi:
Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD.
Trả lời:
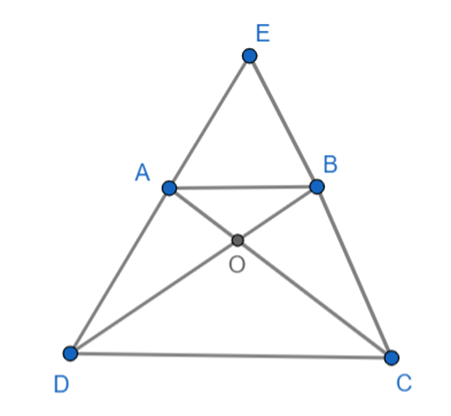
Xét ∆ADC và ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
(gt)
DC chung
Do đó: ∆ADC = ∆BCD (c.g.c) ⇒
Trong ∆OCD ta có:
⇒ ∆OCD cân tại O
⇒ OC = OD (1)
AC = BD (tính chất hình thang cân)
⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
Vậy OA = OB; OC = OD.
b) Theo phần a có: OA = OB
∆ADC = ∆BCD (c.g.c)
⇒ ∆EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (tính chất hình thang cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.